Praktikumsprotokoll Kernzerfall

Kernzerfall

Inhaltsverzeichnis

Abbildungsverzeichnis

Tabellenverzeichnis

1. Grundlagen

1.1. Versuchseinleitung

1.2. Alphastrahlung

1.3. Betastrahlung

1.4. Gammastrahlung

1.5. Geiger-Müller-Zählrohr

1.6. Radioaktives Zerfalls- und Absorptionsgesetz

1.7. Gauß- und Poissonverteilung

2. Auswertung

2.1. Dunkelrate

2.2. Zählrate in Abhängigkeit der Hochspannung

2.3. Statistische Schwankungen der Zählrate

2.4. Absorption der Gammastrahlung

3. Diskussion

3.1. Diskussion und Vergleich mit Literaturwerten

3.2. Verbesserungsmöglichkeiten

4. Zusammenfassung

Quellenverzeichnis

Messprotokoll

Abbildung 1: Zählrate in Abhängigkeit der Spannung

Abbildung 2: Zählrate bei 12 cm Abstand

Abbildung 3: Zählrate bei 8 cm Abstand

Abbildung 4: Zählrate mit Bleiplatten

Abbildung 5: LN der Zählrate mit Bleiplatten

Abbildung 6: Zählrate mit Eisenplatten

Abbildung 7: LN der Zählrate mit Eisenplatten

Tabellenverzeichnis

Tabelle 1: Häufigkeiten

Tabelle 2: Zählraten

1. Grundlagen

1.1. Versuchseinleitung

In diesem Versuch geht es darum, sich mit den Ursachen von radioaktiver Strahlung und den daraus resultierenden Folgen vertraut zu machen. Außerdem soll der Aufbau, die Funktionsweise und der Umgang mit dem Geiger-Müller-Zählrohr betrachtet werden.

1.2. Alphastrahlung

Ein Großteil aller Atomkerne sind radioaktiv, das heißt sie zerfallen unter Aussendung von Elektronen, Photonen, Neutronen oder –Teilchen. Dieser Zerfall entsteht aufgrund der Instabilität von Atomkernen, welche sich durch das Aussenden der Teilchen oder elektromagnetischen Wellen stabilisieren. Man unterscheidet dabei zwischen -Strahlung, -Strahlung und –Strahlung. Während bei - und -Strahlung die Ausstrahlung stets mit einer Kernumwandlung verbunden ist, führt –Strahlung dazu, dass die Kerne von einem angeregten Zustand in einen energieärmeren Zustand übergehen. Bei der -Strahlung handelt es sich um eine ionisierende Teilchenstrahlung, die dann auftritt, wenn der Atomkern beim Zerfall einen  Kern aussendet. Beim Aussenden verringert sich die Kernladungszahl Z des Kerns um zwei und seine Massenzahl A um vier:

       (1.2.1)

dabei steht X für das Mutternuklid, Y für das Tochternuklid und  für die freigesetzte Energie. Das –Teilchen wird aufgrund gleicher Ladungen elektrisch abgestoßen und gleichzeitig durch die Anziehungskraft der Neutronen und Protonen des Kerns angezogen. Dadurch entsteht der Coulombwall, welcher eine Art Barriere darstellt, die durch das Teilchen nicht durchdrungen werden kann, da der Coulombwall über eine höhere Energie als das –Teilchen verfügt. Man kann die Höhe des Coulombwalls  berechnen mit der Gleichung:

      (1.2.2)

wobei  und  für die Kernladungszahlen des Projektils und des Ziels stehen. Aufgrund des sogenannten Tunneleffekts ist es dem Teilchen allerdings dennoch möglich sich kurzfristig innerhalb der Barriere aufzuhalten oder sie nach außen zu verlassen. Für diesen Effekt existieren zwei Erklärungsmöglichkeiten. Die Erste ist die heisenbergsche Unschärferelation, bei der sich, einfach ausgedrückt, das Teilchen kurzfristig eine kleine Menge zusätzlicher Energie ausleiht, damit den Coulombwall überwindet und anschließend die Energie zurückgibt. Berechnet wird sie mit der Gleichung:

  (1.2.3)

wobei  für die Unsicherheit der Impulsangabe,  für die Unsicherheit der Ortskoordinate und h für das plancksche Wirkungsquantum steht. Dabei wird das Wirkungsquantum mit der Formel:

         (1.2.4)

berechnet. Dabei ist p der Impuls und  die Wellenlänge des Teilchens. Die Zweite Erklärung geht von der Schrödingergleichung aus einer Welle, welche angibt wo sich ein Teilchen aufhalten kann. Dabei dringt diese Welle in den Coulombwall ein und verliert exponentiell an Energie. Ist der Wall jetzt klein genug, so bleibt auf seiner anderen Seite noch ein gewisser Rest der Welle übrig. Da nun der Betrag der Wellenfunktion in der Quantenmechanik eine Wahrscheinlichkeit angibt, mit der das Teilchen auf der anderen Seite der Barriere ankommt, kann das Teilchen so den Coulombwall überwinden. Berechnet wird die Schrödingergleichung mittels der Formel:

       (1.2.5)

bei der H für den Hamilton-Operator, E für den Energie-Eigenwert des Operators und  für die Wellenfunktion steht. Der Hamilton-Operator wird berechnet mit der Gleichung:

    (1.2.6)

wobei  die Naturkonstante, welche mit dem planckschen Wirkungsquantum verbunden ist, V die potenzielle Energie, m die Masse und  den Nabla-Operator darstellt. Der Energie-Eigenwert wird mit der Formel:

   (1.2.7)

berechnet. Aufgrund ihrer, vergleichsweise, hohen Masse von  dringen die –Teilchen kaum in Materie ein. Die genaue Reichweite, beziehungsweise Eindringtiefe, hängt dabei von der Energie des –Teilchens ab. Innerhalb von Luft und normalem Druck, beträgt seine Reichweite zwischen 5 cm und 10 cm, erhöht sich aber mit sinkendem Druck. Die Eindringtiefe in Materie, wie zum Beispiel in Wasser oder den menschlichen Körper, beträgt etwa 30 µm bis 50 µm, wodurch bereits ein dickes Blatt oder ein Pullover reicht, um sich vor dieser Strahlung zu schützen. Bei einer Äußeren Einwirkung der -Strahlung ist diese normalerweise ungefährlich, da sie selten die Kleidung durchdringt und bei einer direkten Wirkung auf die Haut nur in die oberen Hautschichten eindringt, welche hauptsächlich aus bereits abgestorbenen Zellen besteht. Bei einem Eindringen in den Körper, beispielsweise durch Einatmen oder Durch Nahrungsaufnahme, ist hingegen mit einer gesundheitsgefährdeten Zellschädigung zu rechnen. Da nun nicht bereits abgestorbene Hautzellen, sondern lebende Zellen, und damit auch Organe, auf engem Raum bestrahlt werden und die dadurch verursachte Belastung zu einem Ausfall der betreffenden Zellen führen kann.

1.3. Betastrahlung

Bei der -Strahlung handelt es sich ebenfalls um eine ionisierende Teilchenstrahlung, besteht aber nicht aus  Kernen, sondern entweder aus Elektronen, bei der -Strahlung, oder seltener aus Positronen, bei der -Strahlung. Dabei existiert das Elektron vorher nicht im Kern, sondern wird durch den Zerfall erzeugt. Des Weiteren wandelt sich eines der Neutronen im Kern in ein Proton um und ein Anti-Neutrino verlässt ebenfalls den Kern. Weiterhin bleibt bei der -Strahlung die Massezahl des Kerns gleich und die Kernladungszahl erhöht sich um eins:

           (1.3.1)

wobei p für Proton und  für Antineutrino steht. Während bei der -Strahlung die Massezahl zwar ebenfalls gleich bleibt, sich allerdings die Kernladungszahl um eins verringert:

           (1.3.2)

dabei steht  für Neutrino. Als Endergebnis des Zerfalls erreicht der Atomkern ein für ihn energiesparenderes Verhältnis durch ein anderes Verhältnis von Neutronen und Protonen. Dadurch wandelt sich Atom auch in ein anderes Element um, welches im Periodensystem um eine Ordnungszahl höher steht. Ihre Reichweite in Luft beträgt dabei einige Zentimeter, wie bei der -Strahlung, bis hin zu einigen Metern, je nachdem wie groß ihre Ausgangsenergie ist. Bei einer äußeren Einwirkung auf den menschlichen Körper kommt es meistens zu schweren Verbrennungen und eventuell zu Folgekrankheiten wie Hautkrebs. Hingegen kommt es bei einer Aufnahme der Strahlung zu den Gleichen gesundheitlichen Schädigung wie bei der –Strahlung und es folgt, bei einer höheren Strahlendosis, eine Erkrankung an Krebs oder Leukämie. Die -Strahlung lässt sich für gewöhnlich bereits mit einer nur einige Millimeter dicken Abschirmung, zum Beispiel einer Plexiglasscheibe, abschirmen. Allerdings wird dabei ein Teil der Energie in –Strahlung umgewandelt, weswegen darauf zu achten ist, dass sich hinter der ersten Abschirmung eine Zweite befindet, um diese Strahlung ebenfalls abzufangen.

1.4. Gammastrahlung

Die –Strahlung ist dabei der Teil der elektromagnetischen Strahlung, welche eine Wellenlänge unter 0,5 nm hat und besteht aus Photonen. Sie entsteht meistens bei  oder  Zerfall, wenn ein Atomkern von einem stark energiehaltigen Zustand in einen energieärmeren Zustand übergeht und sich dabei weder die Neutronenanzahl noch die Anzahl der Protonen ändert. Ob ein Atomkern sich in einem stark energiehaltigen Zustand befindet, erkennt man entweder daran dass er rotiert oder gegenüber der energiesparendsten Form, meistens die Kugelform, verformt ist. Des Weiteren wechselwirkt sie, aufgrund ihrer hohen Energie und elektrischen Neutralität, auch deutlich weniger mit Materie und erhöht damit drastisch die Strahlungsstärke. Des Weiteren kann keine genaue Eindringtiefe oder Reichweite angegeben werden, da durch Absorptionsmaterial, oftmals Blei oder dicker Beton, nur eine Schwächung der Strahlungsintensität erreicht werden kann. Der Grad der Abschwächung ist dabei abhängig von der genauen Wellenlänge der Strahlung und der Kernladungszahl des abschirmenden Materials. Bei einer Verstrahlung von organischem Material kommt es meistens nicht zu einer sofort sicht- oder bemerkbaren Schädigung. Allerdings entstehen Schäden am Erbgut und an den Zellen, welche eine korrekte Zellteilung, Fortpflanzung oder Zellreproduktion stören. Dies führt langfristig zu Tumoren, Krebs, Missbildung der Nachkommen oder ähnlichen Krankheiten.

1.5. Geiger-Müller-Zählrohr

Das Geiger-Müller-Zählrohr ist ein robustes und zuverlässiges Gerät zum Nachweis von radioaktiver Strahlung. Sein wichtigstes Bauteil ist dabei das Zählrohr, siehe auch Abbildung 2, welches beispielsweise aus Glas, Kupfer, Aluminium oder Eisen besteht und mit einem Edelgas, welches auch als Zählgas bezeichnet wird, gefüllt ist. Je nachdem welche Strahlungsarten man messen möchte, sind die Enden des Rohres mit unterschiedlichen Materialien verschlossen. Weiterhin befindet sich im Inneren ein Wolframdraht, auch Zähldraht genannt, welcher den Pluspol darstellt, das Zählrohr hingegen ist der Minuspol. Außerdem ist der Innendruck geringer als der Atmosphärendruck auf Meereshöhe. Nun wird das Zählrohr an den Minuspol einer Spannungsquelle von mehreren hundert Volt angeschlossen und anschließend über einen Widerstand im Megaohm Bereich mit dem Wolframdraht verbunden. Dadurch entsteht um den Draht im Inneren der Röhre ein zylindrisches und symmetrisches elektrische Feld. Des Weiteren wird die Spannung am Widerstand abgegriffen, anschließend mit einem Verstärker im Digitalzähler verstärkt und schließlich die Anzahl der Spannungsimpulse gezählt. Wenn nun radioaktive Strahlung in das Rohr gelangt, dann sorgt sie für eine Ionisierung des Gases längs ihrer Spur, wodurch bei niedriger Spannung Elektron-Ion-Paare entstehen, dies wird auch der Rekombinationsbereich genannt, siehe dazu auch Abbildung 3. Erhöht man nun die Spannung, dann werden, aufgrund des elektrischen Feldes, die leichten Elektronen zum starken Bereich des elektrischen Feldes, also zum Draht, und die trägen Ionen zur Zählrohrwand gezogen werden, was auch als Proportionalbereich bezeichnet wird. Dabei werden die Ionen leicht und die Elektronen stark beschleunigt. Wobei die beschleunigten Elektronen neue Elektron-Ion-Paare bilden, welche dann ebenfalls vom Draht angezogen und beschleunigt werden und ebenfalls neue Elektron-Ion-Paare bilden. Weiterhin entstehen, aufgrund der großen Elektronenbeschleunigung, zusätzlich noch Photonen. Deren Bewegung ist dabei nicht an den elektrischen Feldlinien gebunden und sie verteilen sich deshalb im gesamten Rohr. Außerdem sorgen die Photonen nun für eine Ionisierung des Edelgases, auch außerhalb der Spur der radioaktiven Strahlung, was wiederum zum Entstehen von weiteren Elektronen sorgt. Dies führt dazu, dass das Rohr nun vollständig von der elektrischen Entladung erfasst wird. Dadurch erhöht sich auch die Anzahl der Spannungsimpulse und es kann so die Strahlungsstärke gegenüber dem Normalwert ermittelt werden. Dies wird dann auch als Plateau- oder Geiger-Müller-Bereich bezeichnet und ist dann der Zählbereich, in dem man die Strahlungsmessung vornimmt. Würde man die zugeführte Spannung nun noch weiter erhöhen, würden die Gasentladungen völlig unkontrolliert ablaufen und so zu einer Beschädigung des Zählrohres führen.

1.6. Radioaktives Zerfalls- und Absorptionsgesetz

Da es nicht möglich ist genau zu bestimmen wann ein instabiler Atomkern zerfällt, aufgrund seines spontanen und rein statistischen Zerfalls, kann man auch seine Lebensdauer nicht exakt bestimmen. Weil sich aber extrem viele, und vor allem gleiche, instabile Kerne innerhalb des radioaktiven Materials befinden, bedeutet dies, dass pro Zeiteinheit immer die gleiche Anzahl an vorhandenen Kernen zerfällt. Die Menge der in dieser Zeiteinheit zerfallenen Kerne lässt sich nun bestimmen mit:

    (1.6.1)

und ist proportional mit der Gesamtzahl an radioaktiven Kernen N und einer Zerfallskonstanten :

   (1.6.2)

wobei t für die vergangene Zeiteinheit steht. Integriert man nun Gleichung 1.3.2, so erhält man:

(1.6.3)

dabei steht  für die Anzahl der am Start der Beobachtung aktiven Kerne und  die Anzahl der Kerne, welche noch nicht zerfallen sind nach dem vergehen der Zeit t. Alternativ kann man diese Gleichung auch beschreiben als:

    (1.6.4)

wobei  der Kehrwert von  ist und für die mittlere Lebensdauer der aktiven Kerne steht. Man erkennt hierbei direkt, dass die Anzahl der stabilen Kerne exponentiell mit der vergangen Zeitspanne, der Zerfallskonstante und der mittleren Lebensdauer abnimmt. Weiterhin kann man die Halbwertszeit  eines Kernes mit der Formel:

          (1.6.5)

bestimmen. Kombiniert man nun die Gleichung 1.3.3 und 1.3.5, so erhält man die Formel:

              (1.6.6)

Möchte man nun noch die von einem Material absorbierte Strahlung berechnen, verwendet man die Formel:

    (1.6.7)

bei der  für den material- und energieabhängigen Absorptionskoeffizienten steht und die die gleiche exponentielle Form wie die Gleichung für das Zerfallsgesetz hat

1.7. Gauß- und Poissonverteilung

Die Gaußverteilung, auch Normalverteilung oder Glockenkurve genannt, ist eine der wichtigsten Verteilungsfunktionen für statistische Berechnungen. Sie besagt, dass die einzelnen Messwerte normalverteilt sind, und damit nahe am Durchschnitt liegen, während nur wenige Messwerte deutlich nach oben oder unten vom Durchschnitt abweichen. Definiert ist sie durch die Gleichung:

         (1.7.1)

wobei µ für den Erwartungswert, welcher festlegt an welchem Punkt die Verteilung ihren Maximalwert annehmen wird, und σ für die Standardabweichung steht. Die Poissonverteilung ist eine weitere Verteilungsfunktion für statistische Berechnungen und Wahrscheinlichkeitsverteilungen und hat eine ähnliche Wichtigkeit wie die Gaußverteilung. Sie findet Verwendung, wenn man die Häufigkeit bestimmter Ereignisse innerhalbe eines gewissen Zeitraumes beobachten möchte, zum Beispiel die Anzahl der –Teilchen, welche ein radioaktives Material pro Sekunde aussendet. Weiterhin ist der Kernzerfall ein statistischer Prozess, also ein Zufälliger, welcher sich mit diskreten Wahrscheinlichkeitsverteilungen berechnen lässt. Die Poissonverteilung ist definiert durch die Formel:

  (1.7.2)

dabei ist  der Erwartungswert, n eine natürliche Zahl ≥ 0 und X die Zufallsvariable der Poissonverteilung. Dabei geht die Poissonverteilung in die Gaußverteilung über, wenn das n sehr groß ist. Des Weiteren kann die Standardabweichung der Poissonverteilung direkt aus dem Erwartungswert berechnet werden und zwar mit der Gleichung:

    (1.7.3)

2. Auswertung

2.1. Dunkelrate

Im ersten Versuchsteil wird die Dunkelrate D, oder auch Nullrate bestimmt, welche im Folgenden in counts per minute (cpm) angegeben wird. Dazu wurde die Zählrate ohne Präparat zehnmal mit einer Spannung von  am Zählrohr gemessen. Es ergibt sich eine mittlere Dunkelrate von. Da die Ereignisse der Poissonverteilung folgen ergibt sich der Fehler aus der Wurzel des Mittelwertes, was zu dem Ergebnis von  führt.

2.2. Zählrate in Abhängigkeit der Hochspannung

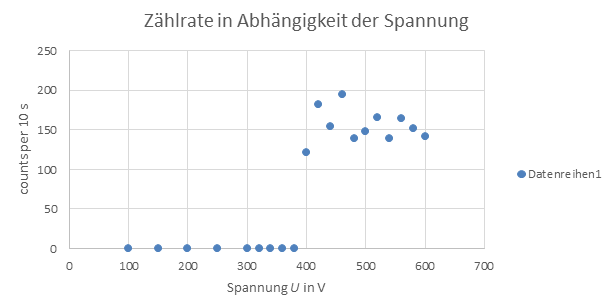
Im zweiten Versuchsteil wurde ein radioaktives Präparat ca. 12 cm vor dem Zählrohr platziert und die Zählrate für jeweils 10 s bei 20 verschiedenen am Zählrohr angelegten Spannungen zwischen 100 V und 600 V gemessen, wobei die Abstände der Spannungen an die zu erwartenden Zählraten angepasst wurden.

^{Abbildung 1: Zählrate in Abhängigkeit der Spannung}

Wie dem Diagramm zu entnehmen ist, wurden unterhalb einer Spannung von 400 V keine Counts gemessen, erst ab 400 V wurden überhaupt Counts gemessen, da freigesetzte Elektronen durch das elektrische Feld so stark beschleunigt wurden, dass weiter Ionisationsprozesse stattfanden, was wiederum einer Gasentladung führte, welche dafür sorgten, dass die einheitlichen Impulse als optisches oder akustisches Signal ausgegeben wurden. In diesem Fall fängt der Plateaubereich also bei 400 V an. Würde man die Spannung noch über die 600 V weiter erhöhen, so würden die Impulse außer Kontrolle geraten und somit das Rohr zerstören. Vom Hersteller werden 500 V Betriebsspannung empfohlen, da sich die Spannung im mittleren Teil des Plateaubereichs befinden und somit ohne Gefahr das Rohr zu zerstören eine gute Detektion erzielt wird.

2.3. Statistische Schwankungen der Zählrate

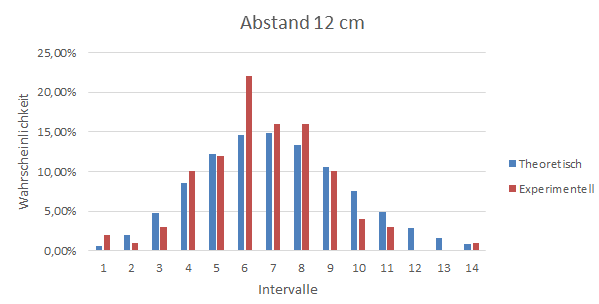
Im dritten Versuchsteil wird die statistische Schwankung der Zählrate untersucht. Dafür wurde mit einer Spannung von 500 V die Zählrate 100 mal für jeweils 10 s gemessen, zuerst im Abstand von 12 cm und anschließend im Abstand von 8 cm. Auf die Messung eines dritten Abstandes wurde aus Zeitgründen verzichtet. Die Anzahl der Counts wurde für beide Abstände in jeweils 14 Intervalle unterteilt. Nun wird der Mittelwert für die Anzahl an Messung  welche im Intervall i liegen gebildet, wobei die Rechnung analog zur Rechnung in 2.1 ist. Daraus ergibt sich . Die prozentuale experimentelle Häufigkeit  der jeweiligen Intervalle ist genau , da jeweils 100 Messungen durchgeführt wurden. Die prozentuale theoretische Häufigkeit , wobei i das Intervall angibt, der jeweiligen Intervalle folgt aus der Poissonverteilung mit der Formel 1.4.2:

Hier die Rechnung beispielhaft für den Abstand von 12 cm und :

^{Tabelle 1: Häufigkeiten}

^{Abbildung 2: Zählrate bei 12 cm Abstand}

^{Abbildung 3: Zählrate bei 8 cm Abstand}

An den Diagrammen kann man erkennen, dass gerade bei den Maxima die experimentellen leicht von den theoretischen Werten abweichen, aber beide experimentellen Kurven haben bereits die Form der theoretischen Kurve.

2.4. Absorption der Gammastrahlung

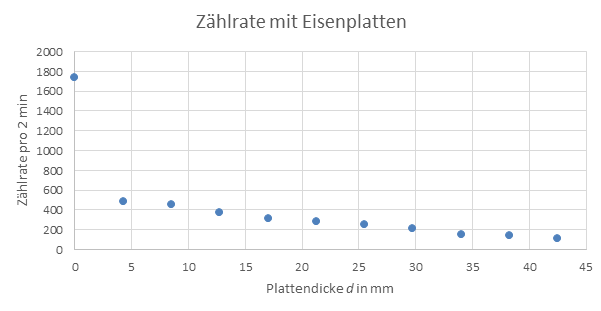
Im vierten Versuchsteil wurde die Absorption der Strahlung durch Blei- und Eisenplatten gemessen. Gemessen wurde erneut mit 500 V Spannung und jeweils 2 min. Den Zählraten I wurde bereits die Dunkelrate abgezogen.

^{Tabelle 2: Zählraten}

^{Abbildung 4: Zählrate mit Bleiplatten}

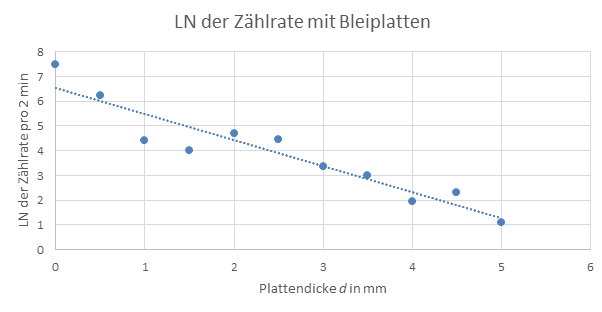
^{Abbildung 5: LN der Zählrate mit Bleiplatten}

Trägt man den Logarithmus der Zählrate über der Plattendicke auf, so kann man eine Ausgleichsgerade erstellen. Die Steigung der Gerade gibt dann den Absorptionskoeffizienten des Materials an. Für Blei wurde dieser mittels SciDAVis ermittelt zu:

^{Abbildung 6: Zählrate mit Eisenplatten}

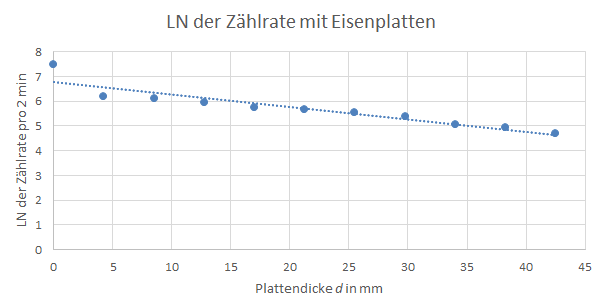
^{Abbildung 7: LN der Zählrate mit Eisenplatten}

Analog zu Blei wurde der Absorptionskoeffizient von Eisen bestimmt zu:

3. Diskussion

3.1. Diskussion und Vergleich mit Literaturwerten

Zu der bestimmten Dunkelrate kann nicht viel ausgesagt werden, da keine Vergleichswerte vorliegen. Die beste Detektion der Strahlung konnte, wie erwartet und in Abschnitt 2.2 beschrieben, in dem Bereich der Spannung um 500 V gezeigt werden und die statistischen Schwankungen sind im Vergleich zu den theoretisch vorhergesagten Werten nicht unerwartet hoch. Mit geringerem Abstand des Detektors zur Probe konnten mehr Counts gemessen werden, allerdings ist die statistische Verteilung unabhängig vom Abstand, wie in Abbildung 5 und 6 zu sehen ist. Zu den Absorptionskoeffizienten von Blei und Eisen kann keine Abweichung oder Übereinstimmung mit Literaturwerten gezeigt werden, da sich die Literaturwerte in Abhängigkeit der Quantenenergie im Bereich zwischen 0,472/cm und 1610/cm für Blei und 0,233/cm und 1415/cm für Eisen befinden und nicht bekannt ist welche Energie die Strahlung im Versuch hatte. Das Blei hat allerdings einen mehr doppelt so hohen Absorptionskoeffizienten wie das Eisen und schirmt somit besser, da Blei eine höhere Dichte besitzt und durch seine höhere Kernladungszahl einen größeren Atomkern besitzt, der die –Strahlung abfangen kann.

3.2. Verbesserungsmöglichkeiten

Um genauere Ergebnisse zu erzielen wäre es für alle Versuchsteile, gerade aufgrund der Zufälligkeit des radioaktiven Zerfalls, hilfreich mehr Messungen durchzuführen. Versuchsteil 3 würde sich dadurch deutlich der Poissonverteilung annähern, allerdings ist es aufgrund der zeitlichen Begrenzung des Versuchs nicht möglich, eine dafür ausreichende Anzahl an zusätzlichen Messungen durchzuführen.

4. Zusammenfassung

In diesem Versuch wurde die Dunkelrate zu

sowie die Absorptionskoeffizienten von Blei und Eisen zu

bestimmt.

Quellenverzeichnis

1. Bergische Universität Wuppertal. (30. April 2015). Abgerufen am 30. April 2015 von Bergische Universität Wuppertal: http://hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/...
2. Geigerzaehler.com. (21. April 2015). Abgerufen am 21. April 2015 von Geigerzaehler.com: http://www.geigerzaehler.com/zaehlrohr/
3. Hemmerich, W. (23. April 2015). MatheGuru. Abgerufen am 23. April 2015 von MatheGuru: http://matheguru.com/stochastik/31-normalverteilung.html
4. Hemmerich, W. (23. April 2015). MatheGuru. Abgerufen am 23. April 2015 von MatheGuru: http://matheguru.com/stochastik/168-poisson-verteilung.html
5. Kleinig, H., & Sitte, P. (1992). Zellbiologie (3. Auflage Ausg.). Gustav Fischer Verlag.
6. Kuchling, H. (2014). Taschenbuch der Physik (21. Auflage Ausg.). München: Carl Hanser Verlag.
7. Müller-Esterl, W. (2011). Biochemie - Eine Einführung für Mediziner und Naturwissenschaftler (2. Auflage Ausg.). Spektrum Akademischer Verlag.
8. Riedel, E. (1994). Anorganische Chemie (3. Auflage Ausg.). Berlin: Walter de Gruyter.
9. Schulz, J. (30. April 2015). Joachims Quantenwelt. Abgerufen am 30. April 2015 von Joachims Quantenwelt: http://www.quantenwelt.de/quantenmechanik/wellenfunktion/schrodingerglei...
10. Sturm, G. (30. April 2015). Quanten.de. Abgerufen am 30. April 2015 von Quanten.de: http://www.quanten.de/unschaerferelation.html
11. Tipler, P. A., & Mosca, G. (2009). Physik (6. Auflage Ausg.). Springer-Verlag.
12. Wikipedia. (29. Mai 2015). Abgerufen am 29. Mai 2015 von Wikipedia: http://de.wikipedia.org/wiki/Z%C3%A4hlrohr