Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls C-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Franck-Hertz Versuch
Inhaltsverzeichnis
1.3. Termschema und Unschärferelation
2.2. Bestimmung des Planckschen Wirkungsquants h
In diesem Versuch geht es darum, die Anregungsenergie von Neon und Quecksilber, sowie das plancksche Wirkungsquantum mittels des Elektronenstoßversuchs zu ermitteln.
Das Bohrsche Atommodell, benannt nach seinem Erfinder Niels Bohr, wurde 1913 veröffentlicht, wobei das rutherfordsche Atommodell als Ausgangspunkt diente. Dabei ist anzumerken, dass das rutherfordsche Atommodell zwar schon eine Einteilung in Elektronen und Protonen besaß und bereits besagte, dass die negativ geladenen Elektronen den positiv geladenen Kern umkreisen, allerdings konnte es einige Gesetzmäßigkeiten der klassischen Elektrodynamik nicht erklären. Denn diese besagt, dass das Elektron während seiner Bewegung Energie in Form von elektromagnetischen Wellen aussendet und, aufgrund des Energieverlustes, früher oder später seine Bahn nicht mehr halten kann und in den Kern stürzen müsste. Im Normalfall sind Atome allerdings stabil und zerfallen nur durch eine vorherige Anregung. Bohr entfernte sich nun, mit seinen Postulaten, von der klassischen Mechanik und Elektrodynamik, wodurch er ein Atommodell erhielt, welches das beobachtete Verhalten von Atomen besser erklären konnte. Nach dem ersten Bohrschen Postulat können die sich bewegenden Elektronen auf bestimmten Bahnen ihre Energie erhalten und werden bestimmt durch die Quantisierung des Elektronenimpulses L mittels der Gleichung:
(1.2.1)
wobei n für die Hauptquantenzahl und für das Planck’sche Wirkungsquant steht. Weiterhin führen die Elektronen, nach dem zweiten Bohrschen Postulat, Quantensprünge durch, bei der sie von einer Atombahn zu einer anderen springen. Dabei wird beim Sprung von einer Bahn mit der Energie zu einer energetisch höheren oder niedrigeren Bahn der Energie , die Energie E in Form von Photonen, mit der Frequenz , frei, woraus sich folgende Gleichung ergibt:
(1.2.2)
Ein Grund für den Bahnwechsel eines Elektrons kann beispielsweiße eine Absorbierung von einem Photon sein, wodurch das Elektron dann in einen angeregteren Zustand, und damit auch in eine andere Schale, übergeht. Bei einer ausreichend großen Energiezufuhr kann das sich das Elektron auch ganz lösen und dadurch das Atom ionisieren. Sollte dafür allerdings nicht ausreichend Energie zur Verfügung stehen, wird es nach einiger Zeit wieder in seinen ursprünglichen Zustand übergehen.
1.3. Termschema und Unschärferelation
Mittels des Termschemas lassen sich die verschiedenen Energieniveaus von Atomen grafisch darstellen. Dabei wird auf die x-Achse die Elektronenanzahl und auf die y-Achse die verschiedenen Energien, Haupt-, und Nebenquantenzahlen aufgetragen. Weiterhin zeigen die Pfeile der Grafik die möglichen Quantensprünge, entsprechen dabei Spektrallinien mit bestimmten Wellenlängen und ihre Länge zeigt die Energiedifferenz des jeweiligen Sprungs. Dabei lassen sich sämtliche Linien, welche auf demselben Energieniveau enden, zu bestimmten Serien zusammenfassen. Diese Darstellung ist allerdings nur eine vereinfachte Version, auf Basis des Bohrschen Atommodells und wird bei Berücksichtigung der Unschärferelation deutlich komplexer. Der Grund für die Berücksichtigung ist der Unterschied zwischen dem Atommodell von Bohr und den experimentellen Betrachtungen, denn während bei einem Wasserstoffatom die Ergebnisse des Bohrschen Atommodell mit denen der Quantenmechanik noch übereinstimmt, ist dies es bei komplexeren Atomen nicht mehr der Fall und chemische Bindungen können so nicht mehr erklärt werden
Der nach James Frank und Gustav Hertz benannte Franck-Hertz-Versuch, stützte das Bohrsche Atommodell und lieferte experimentelle Beweise für die Quantentheorie. Der Versuch besteht dabei aus einem Glaskolben, welcher ein Vakuum enthält und mit Neon oder gasförmigen Quecksilber gefüllt wird. Weiterhin befinden sich in dem Kolben eine Kathode, ein Gitter und eine Auffangelektrode. Durch die Kathode werden die Elektronen, mittels der Zufuhr thermischer Energie, gelöst und anschließend durch das, zwischen der Kathode und dem Gitter, anliegenden elektrischen Feld beschleunigt. Kurz vor dem Gitter erreichen sie dann ihre maximale Geschwindigkeit und landen größtenteils auf dem Gitter, wodurch sie zur Kathode zurück transportiert werden und dabei die Stromquelle passieren. Der verbleibende kleine Teil der Atome, welcher das Gitter passiert, wird anschließend durch die Auffangelektrode abgebremst und eingefangen. Anschließend werden sie ebenfalls zurückgeschickt, wobei sich der dadurch auftretende Anodenstrom in Abhängigkeit der Beschleunigungsspannung messen lässt und man dann damit eine Kurve wie in Abbildung 4 erhält. Wie in der Abbildung zu sehen ist, steigt der Strom zuerst mit der Spannung an und fällt anschließend wieder, bevor er erneut ansteigt. Der Grund dafür ist, dass die Elektronen durch die Beschleunigung zwischen der Kathode und Anode eine bestimmte kinetische Energie erreichen, welche ab einer gewissen Intensität zu Stößen zwischen den Elektronen und dem Gas führt. Während diese Stöße bei einer geringen kinetischen Energie nur elastisch sind, führen sie bei höheren Energien zu einem Energieverlust, wodurch die Elektronen das Bremspotential nicht mehr überwinden können und es so zu einem Absinken des Stroms kommt. Dabei gehen dann die Atome von ihrem angeregten Zustand wieder in ihren Grundzustand über, wodurch sie sichtbares Licht aussenden. Wird nun die Spannung weiter erhöht, so erhöht sich die kinetische Energie wieder, die Elektronen können erneut das Bremspotential überwinden und es erfolgt wieder ein Anstieg des Stroms. Die Energie des ausgesendeten Lichtes kann also berechnet werden mit der Formel:
(1.4.1)
wobei e für die Elementarladung steht. Die Energie ist aber auch gegeben durch die Gleichung:
(1.4.2)
Außerdem kann man die Frequenz mit der folgenden Formel bestimmen:
(1.4.3)
dabei ist c die Lichtgeschwindigkeit und die Wellenlänge. Setzt man nun (1.4.1) und (1.4.2) gleich, setzt (1.4.3) ein und stellt nach um, so erhält man die Gleichung:
(1.4.4)
mit der man jetzt das Plancksche Wirkungsquantum berechnen kann.
Zu Beginn des Versuchs wurde die Franck-Hertz Röhre mit Quecksilber, wie in der Versuchsanleitung beschrieben aufgebaut und die Temperatur auf etwas über 170 °C eingestellt um das Quecksilber verdampfen zu lassen. Auf der X-Achse des Schreibers wurde die angelegte Beschleunigungsspannung in Zehnteln aufgetragen, während der auf der Y-Achse aufgetragene Wert proportional zum Anodenstrom ist. Die Skalierung des Schreibers wurde so eingestellt, dass sich die Graphen gut auf ein DIN A4 Blatt zeichnen ließen. Die eingestellte Skalierung ist dem Messprotokoll zu entnehmen, die Werte sind aber scheinbar nicht ganz korrekt, weshalb die Beschleunigungsspannung alle 5 V kurz auf diesem Wert stehen gelassen wurden. Diese Markierungen sind auf den Graphen breiter und dunkler als der Rest der Graphen zu erkennen. Am PC wurde auf den eingescannten Graphen der Abstand auf der X-Achse der Markierungen gemessen und anschließend gemittelt und die doppelte Standardabweichung des Mittelwertes als Fehler verwendet, womit ein Skalierungsfaktor von folgt. Der Skalierungsfaktor der Y-Achse ist für diesen Versuch zweitranging und kann aufgrund von fehlenden Referenzwerten auch nicht näher bestimmt werden. Im letzten Versuchsteil wurde statt der Quecksilberröhre eine Röhre mit Neon verwendet.
Wie zu erwarten war steigt der Strom mit dem Erhöhen der Beschleunigungsspannung, allerdings treten bei bestimmten Spannungen Peaks auf, nach denen der Strom wieder sinkt. Der Grund dafür ist, dass die beschleunigten Elektronen mit höherer Spannung mehr Energie besitzen und ab einer bestimmten Spannung genug Energie besitzen um beim Stoß mit einem Atom dieses anzuregen. Die benötigte Menge an Energie ist durch die diskreten Energieniveaus gegeben, also gibt es keine kontinuierliche Energieabgabe der Elektronen. Geben die Elektronen bei einem Stoß Energie ab, so sinkt der Strom wieder, erhöht man die Beschleunigungsspannung allerdings weiter, so besitzen die Elektronen beim zweiten Peak genügend Energie um 2 Atome anzuregen, wonach der Strom wieder sinkt. Dieser Vorgang wiederholt sich mit zunehmender Beschleunigungsspannung. Vergleicht man die Kurven von Quecksilber mit den Kurven des Neons, so fällt auf, dass die Peaks bei Neon weiter auseinander liegen, was bedeutet, dass bei Neon mehr Energie nötig ist um diese anzuregen.
2.2. Bestimmung des Planckschen Wirkungsquants h
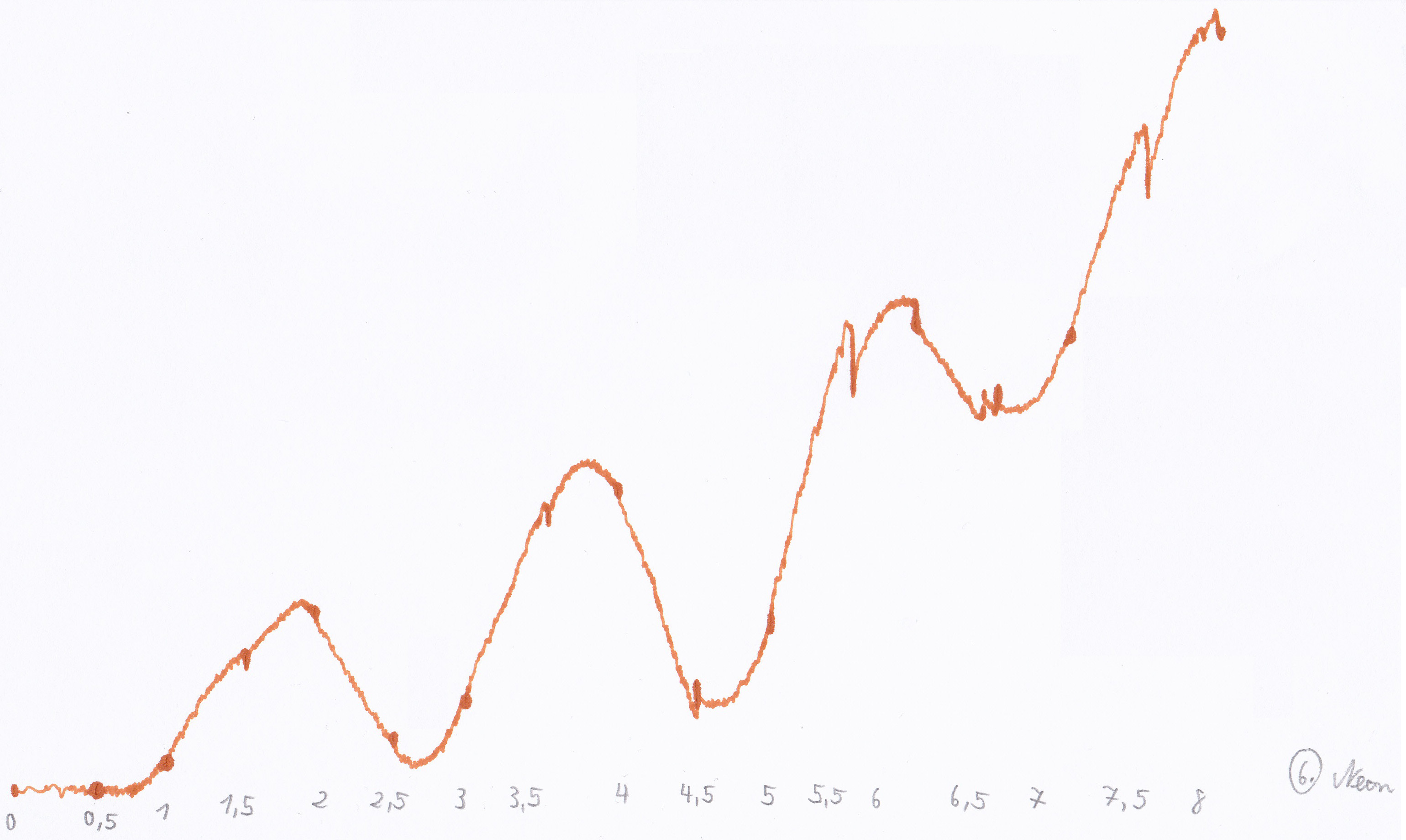
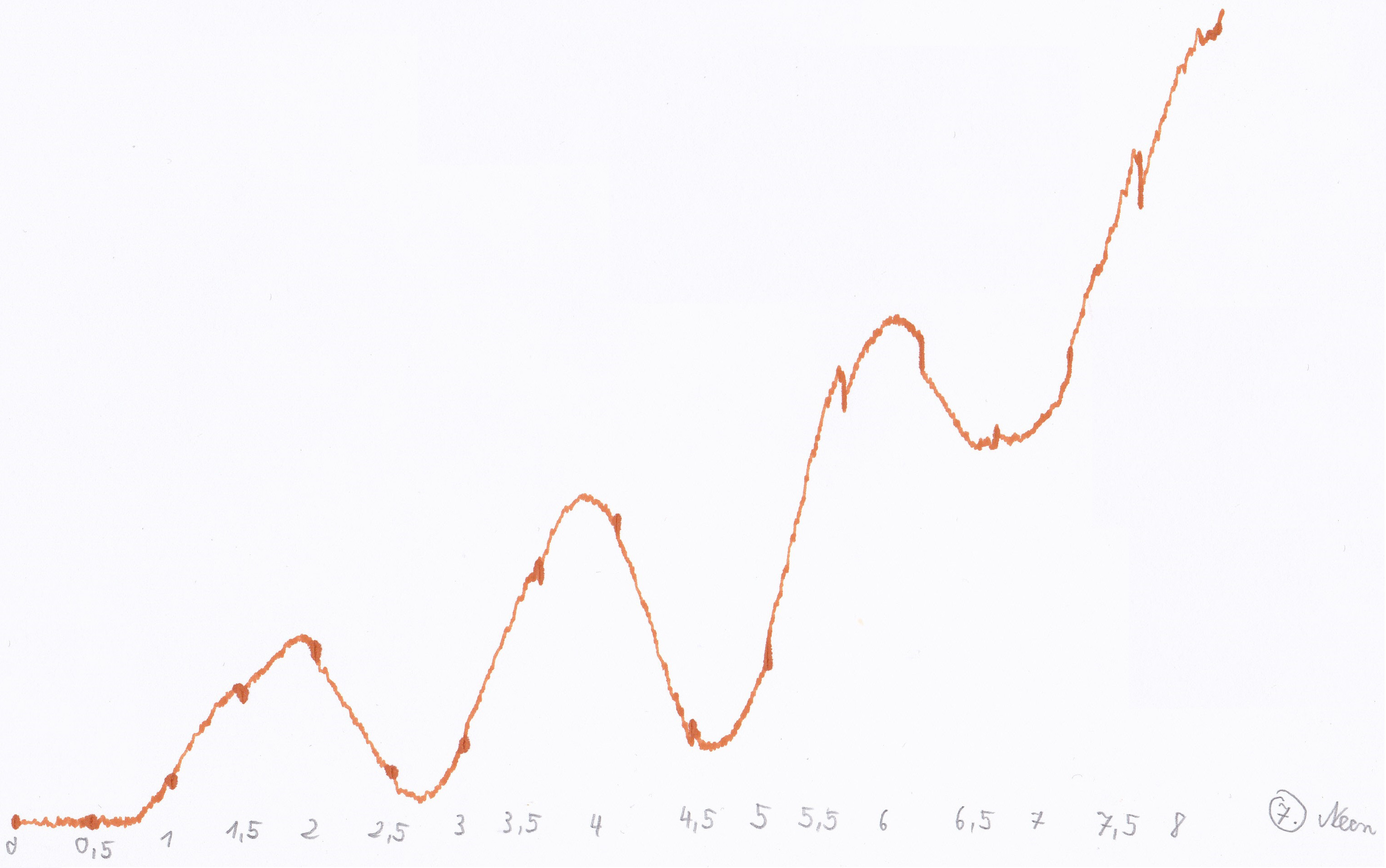
Um die Spannungen zu berechnen wurden zunächst am PC für alle Kurven die Abstände der Peaks gemessen, dafür wurden die Peaks mit einem Strich markiert und die Abstände zwischen den Strichen auf der X-Achse gemessen. In der folgenden Abbildung sind die Markierungen für die zweite Messung zu sehen:
Abbildung 1: Zweite Messung
Alle gemessenen Abstände d der Kurven sind in Tabelle 1 zu finden.
|
d in Pixel |
||||||||||
|
1 |
160 |
175 |
145 |
165 |
169 |
165 |
166 |
159 |
169 |
159 |
|
2 |
157 |
158 |
173 |
152 |
160 |
169 |
165 |
166 |
|
|
|
3 |
160 |
161 |
141 |
185 |
163 |
158 |
168 |
166 |
167 |
|
|
4 |
630 |
715 |
|
|
|
|
|
|
|
|
|
5 |
624 |
697 |
|
|
|
|
|
|
|
|
|
6 |
626 |
691 |
|
|
|
|
|
|
|
|
|
7 |
622 |
690 |
|
|
|
|
|
|
|
|
Tabelle 1: Gemessene Abstände und Mittelwerte
Für alle Abstände von Quecksilber wurde der Mittelwert berechnet zu und die doppelte Standardabweichung mit . Für Neon ergibt sich ein Mittelwert von und als Fehler die größte Abweichung zwischen Messwert und Mittelwert mit . Damit ergeben sich für die Abstände und . Mit können nun die Spannungsdifferenzen zwischen den Peaks berechnet werden, eine Beispielrechnung erfolgt für die erste Spannung:
Damit ergeben sich für die Spannungsdifferenzen und . Nun kann das Plancksche Wirkungsquant h mit Formel (1.4.4) mit den Spannungen von Quecksilber, der Wellenlänge des vom Quecksilber ausgesendeten Lichts aus der Versuchsanleitung , der Elementarladung und der Lichtgeschwindigkeit berechnet werden. Hier eine Beispielrechnung für die erste Messung:
Damit ergibt sich ein Gesamtwert von
2.3. Bestimmung der Anregungsenergie
Mit den zuvor berechneten Spannungen und der Elementarladung kann nur mit Formel (1.4.1) die Anregungsenergie bestimmt werden. Hier eine Beispielrechnung:
Damit ergeben sich die beiden Anregungsenergien
Die Formeln (1.4.2) und (1.4.3) können umgestellt werden zu und mit kann nun die zu Neon gehörige Wellenlänge berechnet werden.
Damit ergibt sich für Neon eine Wellenlänge von . Licht dieser Wellenlänge ist für das menschliche Auge nicht sichtbar, trotzdem wurde beim Versuch orange bis rötliches Licht gesehen. Es ist daher anzunehmen, dass das Neon nicht direkt in den Grundzustand überging, sondern über mehrere Zustände wie im Termschema zu sehen, Licht im gelb bis roten Bereich und im ultravioletten Bereich aussendet.
Der in diesem Versuch bestimmte Wert des Planckschen Wirkungsquants stimmt mit dem Literaturwert [5] von unter Berücksichtigung des Fehlers überein. Für die Anregungsenergie von Neon mit zeigt sich im Vergleich mit dem Termschema aus der Versuchsanleitung, dass diese mit der Ionisierungsspannung von 21,5 eV übereinstimmt. Auch die Anregungsenergie von Quecksilber mit stimmt mit dem Literaturwert [1] von überein. Mögliche Fehler bei der Auswertung könnten dadurch entstanden sein, dass der Drehregler der Beschleunigungsspannung von Hand nicht sehr konstant gedreht werden konnte, wodurch sich kleine Spitzen in den Graphen bildeten. Außerdem scheinen die Graphen Sprünge an den Stellen zu machen, wo die Spannung für eine kurze Zeit konstant gehalten wurde, was eventuell zu Verfälschungen der Messwerte geführt haben könnte.
In diesem Versuch wurde das Plancksche Wirkungsquant bestimmt zu
sowie die Anregungsenergien von Quecksilber und Neon zu
- Albert-Ludwigs-Universität Freiburg. (25. Juli 2015). Abgerufen am 25. Juli 2015 von Albert-Ludwigs-Universität Freiburg: http://ruby.chemie.uni-freiburg.de/Vorlesung/methoden_I_2.xhtml
- Bergische Universität Wuppertal. (1. Juli 2015). Abgerufen am 1. Juli 2015 von Bergische Universität Wuppertal: http://hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase…
- ChemgaPedia. (1. Juli 2015). Abgerufen am 1. Juli 2015 von ChemgaPedia: http://www.chemgapedia.de/vsengine/tra/vsc/de/ch/13/trajektorien/aas.tr…
- Georg-August-Universität Göttingen. (1. Juli 2015). Abgerufen am 1. Juli 2015 von Georg-August-Universität Göttingen: https://lp.uni-goettingen.de/get/text/1628
- Kuchling, H. (2014). Taschenbuch der Physik (21. Ausg.). München: Carl Hanser Verlag.
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Ausg.). Springer-Verlag.
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Auflage Ausg.). Springer-Verlag.
- Wikipedia. (1. Juli 2015). Abgerufen am 1. Juli 2015 von Wikipedia: https://de.wikipedia.org/wiki/Franck-Hertz-Versuch