Praktikumsprotokoll Gasthermometer

Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.

Gasthermometer

Inhaltsverzeichnis

Abbildungsverzeichnis

Tabellenverzeichnis

1. Grundlagen

1.1. Ideale und reale Gase

1.2. Isotherme, Isobare, Isochore, Stoffmenge und Avogadrozahl

1.3. Nullter Hauptsatz der Thermodynamik und absolute Temperatur

1.4. Druckabhängigkeit des Siedepunktes

1.5. Vor- und Nachteile eines Gasthermometers

2. Auswertung

2.1. Druckabhängigkeit des Siedepunktes

2.2 . Berechnung der Zimmertemperatur

2.3. Berechnung der Raumtemperatur mit Einbeziehung des schädlichen Volumens

3. Diskussion

4. Zusammenfassung

Quellenverzeichnis

Messprotokoll

Abbildungsverzeichnis

Abbildung 1: Temperatur-Druck-Diagramm

Tabellenverzeichnis

Tabelle 1: Messwerte

1. Grundlagen

1.1. Ideale und reale Gase

Ein idealisiertes Gas ist eine Vereinfachung von einem realen Gas, um dieses Gas einfacher berechnen zu können. Es existieren dabei primär drei große Unterschiede zwischen den Gasen. Bei einem idealisierten Gas werden alle Gasteilchen als Massepunkte ohne Ausdehnung angenommen und die Stöße untereinander, beziehungsweise zwischen den Wänden des Gasbehälters sind immer ideal elastische Stoßvorgänge. Weiterhin wird der mittlere Abstand zwischen den Teilchen als sehr viel größer als der Teilchendurchmesser angenommen. Über diese Eigenschaften verfügen reale Gase normalerweise nicht, allerdings lässt es sich mit diesen Vereinfachung deutlich leichter rechnen und die Ergebnisse sind für die weitere Verwendung meistens präzise genug. Berechnet werden sie mit den folgenden Zustandsgleichungen:

   (1.1.1)

Dabei steht p für den Druck, V für das Volumen, n die Stoffmenge, R die universelle Gaskonstante, T für die Temperatur in Kelvin, m die Masse des Gases, N für die Teilchenzahl,  für die spezifische Gaskonstante und  für die Boltzmann-Konstante. Wie bereits erwähnt verfügen reale Gase normalerweise nicht über diese Eigenschaften von idealen Gasen. Wenn man von ihnen allerdings nur eine niedrige Konzentration hat und diese auf eine hohe Temperatur erhitzt, dann verhalten sie sich auch wie ein ideales Gas. Das liegt daran, dass der mittlere Abstand dann deutlich größer als der Teilchendurchmesser, die kinetische Energie deutlich größer als die Bindungsenergie ist und die Stoßkräfte deutlich größer als die Anziehungskräfte sind. Die realen Gase können mit der Van-der-Waals-Zustandsgleichung ebenfalls näherungsweise berechnet werden. Die Gleichung lautet:

             (1.1.2)

 steht dabei für das molare Volumen, a für den Kohäsionsdruck und b für das Kovolumen, wobei a und b materialabhängige Werte sind.

1.2. Isotherme, Isobare, Isochore, Stoffmenge und Avogadrozahl

Isotherme werden in der Thermodynamik verwendet, um das Verhältnis des Volumens und des Drucks, bei konstanter Temperatur, abzubilden. Errechnet werden die jeweiligen Linien, in dem man die Gleichung:

      (1.2.1)

verwendet. Ein noch erwähnenswerter Sonderfall, ist der sogenannte kritische Punkt. Bei diesem Punkt im pV-Diagramm stimmen, bei einem realen Gas, die Eigenschaften für gasförmig und flüssig überein. Das heißt, es existiert kein Unterschied mehr zwischen Flüssigkeit und Dampf. Dieser Punkt befindet sich genau da, wo der Gasdrucks  und der Flüssigkeiten Drucks  genau übereinstimmen. Isobare hingegen bilden die Änderung der Temperatur und des Volumens ab, während der Druck konstant bleibt. Errechnet werden die dazugehörigen Linien des Diagramms mit der Gleichung:

             (1.2.2)

Daraus folgt dann auch, dass die absoluten Temperaturen und Volumen sich proportional zueinander verhalten:

              (1.2.3)

Isochore beschreiben nun die letzte Kombination zwischen fester Temperatur, Druck und Volumen. Bei ihnen bleibt das Volumen immer gleich und es ändern sich der Druck und die Temperatur. Die Diagrammlinien werden hier berechnet mit der Formel:

             (1.2.4)

Daraus folgt dann, ähnlich wie bei den Isobaren, dass eine Druckänderung sich proportional zur Temperaturänderung, und ebenfalls anders herum, verhält:

             (1.2.5)

Die Stoffmenge n gibt an, wie viele Teilchen N eines bestimmten Stoffes sich in einer vorhandenen Stoffprobe befinden. Sie wird in Mol angegeben und enthält  Teilchen, was identisch mit der Avogadro-Konstante  ist. Die Zahl der Einzelteilchen ist offiziell definiert durch die Anzahl der Atome, welche sich in 12 g  befinden. Ermittelt wird sie mit der Formel:

              (1.2.6)

M steht dabei für die Molmasse des Stoffes. Die Avogadro-Konstante kann, mit Hilfe der Stoffmenge, berechnet werden mittels der Gleichung:

            (1.2.7)

1.3. Nullter Hauptsatz der Thermodynamik und absolute Temperatur

Der Nullte Hauptsatz, auch Gesetz des thermischen Gleichgewichts, besagt, dass wenn sich ein System A mit einem System B im thermischen Gleichgewicht befindet und das System B sich mit einem System C auch im thermischen Gleichgewicht befindet, dann befindet sich auch automatisch System A mit System C im thermischen Gleichgewicht.

Die absolute Temperatur, ist ein Temperaturwert, welcher sich auf den absoluten Nullpunkt der Temperatur bezieht. Dieser Nullpunkt ist auch der Bezugspunkt der Kelvinskala und wird dementsprechend in Kelvin gemessen. Um die Temperatur von Grad Celsius in Kelvin, bzw. von Kelvin in Grad Celsius umzurechnen, wird folgende Umrechnung verwendet:

    (1.3.1)

Grund für diesen Umrechnungswert ist die Tatsache, dass der Nullpunkt der Kelvinskala mit ­273,15 °C gleichzusetzen, beziehungsweiße der Nullpunkt der Celsiusskala bei 273,15 K liegt.

1.4. Druckabhängigkeit des Siedepunktes

Der Siedepunkt einer Flüssigkeit ist abhängig von dem Druck, welche auf diese Flüssigkeit wirkt. Der Grund dafür ist die Tatsache, dass die Moleküle der Flüssigkeit die Anziehungskräfte der anderen Moleküle überwinden müssen, um sich so in Gas umzuwandeln. Diese benötigte Kraft steigt mit dem Luftdruck an, welcher auf die Flüssigkeit wirkt, denn je höher der Druck, desto stärker werden die Moleküle zusammen gedrückt. Daraus folgt dann auch direkt, je niedriger der Druck, desto weniger Kraft muss aufgebracht werden um die Anziehungskräfte zu überwinden und sich in Gas zu wandeln und somit reduziert sich auch die Temperatur des Siedepunktes.

1.5. Vor- und Nachteile eines Gasthermometers

Die Vorteile des Gasthermometers sind die hohen Temperaturunterschiede, welche damit gemessen werden können und die Unabhängigkeit von speziellen Stoffeigenschaften. Nachteilig hingegen wirkt sich die Tatsache aus, dass ein Gas verwendet werden muss, welches annähernd den Eigenschaften eines idealen Gases entspricht. Bei der Verwendung eines realen Gases, welches diese Eigenschaften nicht erfüllt, kann es sonst zu deutlichen Messabweichungen kommen. Weiterhin muss während der Messung entweder das Volumen oder der Druck konstant gehalten werden.

2. Auswertung

2.1. Druckabhängigkeit des Siedepunktes

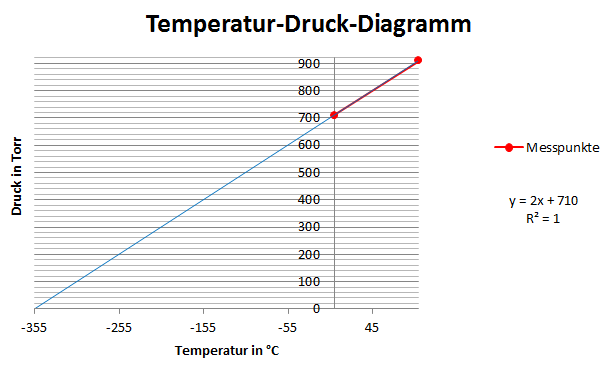
Um die Siedetemperatur von Wasser zu bestimmen wurde der Luftdruck  mit Hilfe eines Barometers gemessen und so ein Wert von 741 Torr ermittelt. Die Siedetemperatur von Wasser entspricht bei diesem Druck circa 99,36 °C oder 372,51 K. Als nächstes wird dann der Druck am Gefrier- und am Siedepunkt benötigt, um damit das Druck-Temperatur-Diagramm zu erstellen. Dazu wird zuerst der Mittelwert der rechnet Höhenwerte, mit der Formel:

         (2.1.1)

errechnet. Anschließend wird die Druckdifferenz während der jeweiligen Temperatur bestimmt, was der Gleichung:

  (2.1.1)

erfolgt. Dabei ist  die linke Steighöhe und  die rechten Steighöhe. Die Ergebnisse für die restlichen Berechnungen können der Tabelle 1 entnommen werden. Da jeder Millimeter einem Torr entspricht, lässt sich die errechnete Differenz direkt auf den Druck übertragen und man erhält so eine Druckdifferenz von 31 Torr für das Eiswasser und 169 Torr für das siedende Wasser. Als nächsten Schritt muss man nun vom Luftdruck die Druckdifferenz des Eiswassers subtrahieren um den Druck bei 0 °C zu ermitteln, beziehungsweise die Differenz bei dem siedenden Wasser addieren um den Druck bei 100 °C zu erhalten. Erstellt man nun mit diesen zwei Messpunkten ein Temperatur-Druck-Diagramm und extrapoliert sie bis zu einem Druck von null Torr, dann schneiden sie die Temperaturachse bei einer Temperatur von -299,43 °C, was -26,28 K entspricht und direkt auf einen Messfehler hindeutet. Aus diesem Diagramm ergibt sich weiterhin die Geradengleichung:

         (2.1.1)

bei der  für die absolute Temperatur steht.

Fehlerrechnung:

Der Gesamtfehler beim Mittelwert für die rechte Höhe setzt sich aus der größten Differenz zwischen Messwert und Mittelwert der jeweiligen Temperatur, sowieso dem systematischen Fehler zusammen. Da die linke Höhe immer gleich hoch eingestellt wurde und auch immer der selber Werte gemessen wurde verändert sich durch eine Mittelwertbildung weder der Wert, noch der Fehler und ist daher nicht notwendig. Für die Höhendifferenz addieren sich beide absoluten Fehler. Addiert oder subtrahiert man nun die Höhen-/Druckdifferenz beim Luftdruck, so addieren sich erneut die absoluten Fehler. Um die Steigung m der Geraden im pT-Diagramm zu bestimmen wird ein Steigungsdreieck verwendet: , wobei  die Differenz der Drücke bei 0 °C und 100 °C,  die Differenz der Temperatur von Eiswasser und siedenden Wasser,  die Temperaturdifferenz zwischen Nullpunkt und absolutem Nullpunkt , und  die Differenz zwischen Druck Null und dem Achsenabschnitt ist, was gleich  ist (Im Folgenden stehen die Indizes E für Eiswasser und S für siedendes Wasser). Der Absolute Nullpunkt berechnet sich nun folgendermaßen:

Der Fehler für den absoluten Nullpunkt berechnet sich nun wie folgt:

Damit ergibt sich für den absoluten Nullpunkt der Messwert:

^{Abbildung 1: Temperatur-Druck-Diagramm}

2.2. Berechnung der Zimmertemperatur

Mit den Berechnungen aus Tabelle 1 und der Geradengleichung, kann man nun die Zimmertemperatur bestimmen. Da die gemessenen Werte für die linke Seite hier wieder größer sind als bei der rechten Seite, muss die Differenz, genau wie beim siedenden Wasser, wieder aufgerechnet werden. Setzt man nun die entsprechenden Werte in (2.1.1) ein, dann folgt daraus eine Raumtemperatur von:

Fehlerrechnung:

Damit ergibt sich ein Messwert für die Zimmertemperatur von:

2.3. Berechnung der Raumtemperatur mit Einbeziehung des schädlichen Volumens

Um das schädliche Volumen  zu berechnen, benötigt man zuerst das Volumen der Kapillare und des Teils des Rohres, welches nicht mit Quecksilber gefüllt ist. Berechnet werden diese beiden Volumina mit den Gleichungen:

 (2.3.1)

und

Aus diesen beiden Volumen ergibt sich dann ein gesamtes schädliches Volumen von:

Um unter Berücksichtigung des schädlichen Volumens die Zimmertemperatur zu bestimmten verwendet man die drei folgenden Varianten von (1.1.1):

   (2.3.2)

   (2.3.3)

     (2.3.4)

Der Index Z steht für die entsprechende Größe bei Zimmertemperatur, der Index x für die Größe bei 0 °C, oder 100 °C. Da die Gesamtteilchenzahl erhalten bleibt und die Summe aus der Teilchenzahl in der Kugel und im schädlichen Volumen ist, kann nun (2.3.2)=(2.3.3)+(2.3.4) gesetzt werden:

             (2.3.5)

Nun wird die Zimmertemperatur mit (2.3.5) zuerst mit Referenzwerten bei 0 °C (bzw. 273,15 K) berechnet:

Mit Referenzwerten bei 100 °C (bzw. 373,15 K):

Fehlerrechnung:

Alle Längen und Durchmesser wurden mit einem Messschieber gemessen, dessen Ungenauigkeit mit  angegeben ist, jedoch sind die Fehler größer geschätzt worden, da die Innendurchmesser relevant sind, aber nur die Außendurchmesser, oder Innendurchmesser nach Augenmaß gemessen werden konnten. Der Fehler der Länge der Kapillare  wurde  besonders groß geschätzt, da diese aus drei  zueinander abgewinkelten geraden Teilstücken besteht. Die Fehler des Durchmessers der Kapillare d und des Durchmessers des Rohrs D wurde  für beide auf  geschätzt. Der Fehler des Volumens der Kapillare und des Rohrs werden beide berechnet mit:

Für den Fehler des schädlichen Volumens addieren sich nun beide Fehler:

Für den Fehler des Volumens des Kugel gilt:

Für den Fehler des Gesamtvolumens addieren sich die Fehler:

Der Fehler der Zimmertemperatur berechnet sich mit folgender Formel:

Für 0 °C ergibt sich ein Fehler von:

Für 100 °C ergibt sich ein Fehler von:

Damit ergeben sich nun folgende Messwerte für die Zimmertemperatur:

4. Zusammenfassung

In diesem Versuch wurde die Zimmertemperatur mit einem Gasthermometer und verschiedenen Auswertungsmethoden bestimmt zu: