Praktikumsprotokoll Spezifische Wärmekapazität von Festkörpern

Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.

 

Spezifische Wärmekapazität von Festkörpern

 

Inhaltsverzeichnis

 

Abbildungsverzeichnis

Tabellenverzeichnis

1. Grundlagen

1.1. Energieformen

1.2. Temperatur und innere Energie

1.3. 1. Hauptsatz der Thermodynamik

1.4. Wärmekapazität und Stoffmenge

1.5. Spezifische und molare Wärmekapazität

1.6. Freiheitsgrade

1.7. Debye-Temperatur

1.8. Regel von Dulong und Petit

1.9. Vierpunktmethode

2. Auswertung

2.1. Bestimmung der Temperaturdifferenzen

2.2. Zugeführte Energie pro Heizschritt

2.3. Spezifische Wärmekapazität

2.4. Molare Wärmekapazität

3. Diskussion

4. Zusammenfassung

Quellenverzeichnis

Messprotokoll

Tabellenverzeichnis

 

Tabelle 1: Temperaturdifferenz der einzelnen Heizphasen

Tabelle 2: Elektrische Energie pro Heizschritt

Tabelle 3: Spezifische Wärmekapazität pro Heizschritt

Tabelle 4: Molare Wärmekapazität

 

1. Grundlagen

 

1.1. Energieformen

 

Unter der Wärmeenergie, auch bekannt als thermische Energie, versteht man die Energie, welche in den Atomen, bzw. Molekülen, eines Stoffes als ungeordnete Bewegung gespeichert ist. Es ist möglich sie zwischen verschiedenen Körpern zu übertragen und zur Berechnung der sich dabei ändernden Energiemenge, wird folgende Gleichung verwendet:

 (1.1.1)

Wobei  die Änderung der Wärmeenergie, m die Masse, c die spezifische Wärmekapazität und  die Temperaturänderung ist. Wenn man Energie in elektrischen Feldern speichert oder mittels Elektrizität überträgt, dann wird dies elektrische Energie  genannt. Sie ist die Fähigkeit des Stromes über einen bestimmten Zeitraum, Wärme zu erzeugen oder eine mechanische Arbeit zu verrichten. Bei konstanter Spannung und Strom, wird die Formel:

 (1.1.2)

verwendet, wenn Spannung und Strom sich mit der Zeit verändern, dann nutzt man das Integral:

       (1.1.3)

um die elektrische Energie zu berechnen. Dabei steht U für Spannung, I für den Strom und t für die Zeit. Die mechanische Energie gibt an wie viel Energie nötig ist, um eine bestimmte Masse von einem Punkt A zu einem Punkt B zu bewegen. Sie setzt sich zusammen aus der kinetischen und der potenziellen Energie. Dabei gibt die kinetische Energie , auch Bewegungsenergie oder Rotationsenergie genannt, die Eigenschaft eines Körpers an, mechanische Arbeit aufgrund seiner aktuellen Bewegung zu verrichten. Berechnet wird sie mit der Gleichung:

        (1.1.4)

wobei v die aktuelle Geschwindigkeit des Körpers ist. Die potenzielle Energie, auch unter dem Namen Lageenergie bekannt, hingegen gibt an, wie viel mechanische Arbeit ein Körper aufgrund seiner aktuellen Lage verrichten kann. Sie wird berechnet mittels der Formel:

         (1.1.5)

Dabei steht g für die Erdbeschleunigung und h für die Höhe. Der gesamte Energiebestand eines bestimmten Systems wird als innere Energie  bezeichnet. Sie setzt sich hauptsächlich aus der thermischen, der chemischen und der Kernenergie zusammen. Dabei ist aber weder die kinetische, noch die potenzielle Energie ein Teil von ihr.

 

1.2. Temperatur und innere Energie

 

Bei einer Änderung der Temperatur, ändert sich auch die Energiemenge der thermischen Energie und diese ist, wie bereits in 1.1 beschrieben, Teil der inneren Energie ist. Daraus folgt dann direkt, dass sich die innere Energie ebenfalls verändert und sie deswegen von der Temperatur abhängig ist. Um nun noch die Temperatur von Grad Celsius in Kelvin, bzw. von Kelvin in Grad Celsius umzurechnen, wird jetzt folgende Umrechnung genutzt:

    (1.2.1)

Grund für diesen Umrechnungswert ist die Tatsache, dass der Nullpunkt der Kelvinskala mit ­273,15 °C gleichzusetzen ist.

 

1.3. 1. Hauptsatz der Thermodynamik

 

Der erste Hauptsatz der Thermodynamik, abgeleitet aus dem Satz der Energieerhaltung, sagt aus, dass die innere Energie eines Systems nur durch den Austausch von Wärme Q und/oder durch Verrichtung einer Arbeit W mit einem anderen System geändert werden kann. Die Änderung der inneren Energie entspricht dabei der zugeführten Wärme und/oder der verrichteten Arbeit. Berechnet wird das Ganze mit der Gleichung:

                     (1.3.1)

 entspricht dabei der Differenz der inneren Energieänderung.

 

1.4. Wärmekapazität und Stoffmenge

 

Unter der Wärmekapazität C versteht man die Aufnahme oder Abgabe der thermischen Energie im Verhältnis zur Temperaturänderung. Berechnet wird das Ganze mit:

            (1.4.1)

Die Stoffmenge n gibt an, wie viele Teilchen eines bestimmten Stoffes sich in einer vorhandenen Stoffprobe befinden. Sie wird in Mol angegeben und enthält  Teilchen, was identisch mit der Avogadro-Konstante  ist. Die Zahl der Einzelteilchen ist offiziell definiert durch die Anzahl der Atome, welche sich in 12 g  befinden. Ermittelt wird sie mit der Formel:

              (1.4.2)

M steht dabei für die Molmasse des Stoffes.

 

1.5. Spezifische und molare Wärmekapazität

 

Mit der spezifischen Wärmekapazität  bezeichnet man die auf die Masse eines bestimmten Stoffes bezogene Wärmekapazität. Oder einfacher ausgedrückt ist es die Menge an Energie, welche man braucht um ein kg von einem bestimmten Stoff um ein K zu erhöhen. Berechnet wird die spezifische Wärmekapazität mit der Gleichung:

                 (1.5.1)

Ähnlich verhält es sich mit der molaren Wärmekapazität , allerdings mit dem Unterschied, dass sie sich nicht auf die Masse, sondern auf die Stoffmenge bezieht. Also wie viel Energie man benötigt, um ein Mol eines Stoffes um ein K zu erhitzen. Sie wird mittels der Formel:

          (1.5.2)

errechnet.

 

1.6. Freiheitsgrade

 

Freiheitsgrade F bezeichnen die verschiedenen Bewegungsmöglichkeiten eines Körpers oder Systems, welche voneinander unabhängig sind. Es können dabei maximale drei Freiheitsgrade auf die Translation, jeweils einen auf die x-, y-, und z-Achse, drei auf die Rotation, auch hier wieder jeweils einen auf die x-, y-, und z-Achse, und sechs auf die Schwingung, jeweils zwei pro x-, y-, und z-Achse, entfallen. Dabei verringert sich die Anzahl der Freiheitsgrade, wenn man die Bewegungsfreiheit des Systems einschränkt. So hat beispielsweise ein Massepunkt, welcher sich frei im Raum bewegen kann, drei Translationsfreiheitsgrade. Zwingt man ihn jetzt aber auf eine vorher bestimmte Kreisbahn, dann verringert sich seine Freiheitsgrade auf einen Einzigen, da er von jedem Punkt innerhalb dieser Bahn, nun nur noch eine Bewegungsrichtung hat.

 

1.7. Debye-Temperatur

 

Die Debye-Temperatur ist eine, im Debye-Modell der Festkörperwärmekapazität, definierte Temperatur. Sie ist ein Maß für jene Temperatur, über die die verschiedenen Schwingungsmoden, beziehungsweiße Freiheitsgrade, innerhalb des Kristalls angeregt werden und unterhalb sie beginnen einzufrieren. Das Unterschreiten und damit auch das Einfrieren sorgt dafür, dass die verschiedenen Freiheitsgrade keinen Beitrag mehr zur Wärme eines Stoffes leisten, während erst bei einer Temperatur welche ausreichend weit über der Debye-Temperatur liegt, das Dulong-Petit Gesetz, siehe 1.8, erfüllt wird. Dabei gilt, je schwerer die Atome und schwächer die Bindung, desto niedriger sind die Schwingungsfrequenzen und damit auch die Debye-Temperatur und je leichter die Atome und je stärker die Bindungen werden, desto höher steigen die Schwingungsfrequenzen und damit ebenfalls die Debye-Temperatur.

 

1.8. Regel von Dulong und Petit

 

Die Regel von Dulong und Petit, auch bekannt als Dulong-Petit Gesetz, besagt dass sämtliche Festkörper über die gleiche molare Wärmekapazität verfügen und diese bei dreimal der universellen Gaskonstante R liegt. Man geht dabei auch von einer gleichmäßigen Anordnung von  Atomen pro Mol aus und das jedes Atom um die Gleichgewichtslage Schwingungen in die Richtungen x, y und z ausführt. Daraus folgt dann, dass die gesamte Energie eines Atoms innerhalb eines Festkörpers definiert ist durch:

                      (1.8.1)

wobei k die Federkonstante einer Bindung und  die Geschwindigkeit ist. Demnach hat jedes Atom des Festkörpers sechs Freiheitsgrade und aus dem Gleichverteilungsgesetz folgt nun, dass die mittlere Atomenergie je Freiheitsgrad  entspricht. Weiterhin gilt:

    (1.8.2)

Da ja, wie bereits beschrieben, eine gleichmäßige Anordnung von  Atomen pro Mol vorhanden ist, kann nun die innere Energie von n Molen eines Festkörpers mit der folgenden Gleichung berechnet werden:

        (1.8.3)

Diese Regel ist allerdings nur gültig bei hohen Temperaturen da, wie bereits in 1.7. beschrieben, bei Temperaturen nahe dem absoluten Nullpunkt sämtliche Freiheitsgrade einfrieren und dadurch die Wärmekapazität gegen null geht.

 

1.9. Vierpunktmethode

 

Die Vierpunktmethode ist ein einfaches Messverfahren, welches sich gut zur Messung von Schicht- und Oberflächenwiderständen eignet. Bei diesem Messverfahren werden vier Elektroden in einer Reihe angeordnet und auf dem zu messenden Werkstoff angebracht. Anschließend wird ein Strom durch die äußeren Spitzen zugeführt, während die inneren Elektroden die Differenz des Potentials auf der Werkstoffoberfläche abtasten. Die Differenz wird dabei durch eine Kompensationsschaltung stromlos erfasst. In Verbindung mit einer Erhitzung des Werkstoffes, kann so eine Änderung des Widerstands im Verhältnis zur Temperaturänderung erfasst werden und damit eine Funktion aufgestellt werden, mit der man die Temperaturänderung abbilden kann.

 

2. Auswertung

 

2.1. Bestimmung der Temperaturdifferenzen

 

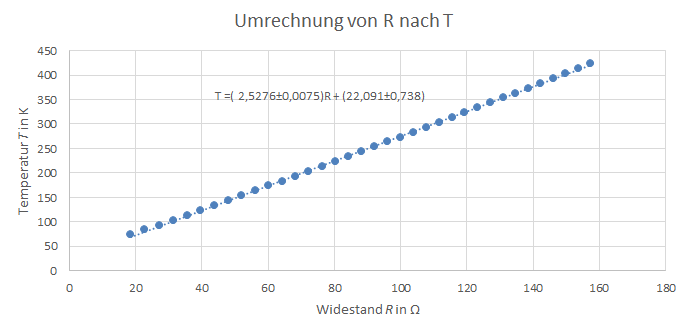
Die Temperatur T bzw. der Widerstand R wurde mit einem Pt-100 Widerstandsthermometer gemessen, wofür eine Ungenauigkeit von  angenommen wird. Zur Bestimmung der Temperatur aus dem Widerstand wurden einige Wertepaare aus der Widerstandstabelle des Pt-100 Widerstandsthermometers entnommen und eine lineare Näherungsgleichung  erstellt, wobei  und  mittels SciDAVis bestimmt wurden. Um die Temperaturdifferenzen  für die i-te Heizphase zu bestimmen, wurden zunächst Näherungsgraden der Form  ,wobei t für die Zeit steht, für alle Nichtheizphasen berechnet und dann die Differenz der i-ten und i+1-ten Näherungsgrade im Mittelpunkt zwischen der i-ten und i+1-ten Nichtheizphase berechnet. Im folgenden Diagramm ist dies beispielhaft dargestellt für die Temperaturdifferenz die aus der ersten Heizphase resultiert.

^{Abbildung 1: Temperaturdifferenz Heizschritt 1}

Die Formel für die Temperaturdifferenz lautet also:

 

wobei  der Mittelpunkt zwischen der i-ten und i+1-ten Heizphase darstellt. Für die Temperaturdifferenz der ersten Heizphase ergibt sich mit dieser Formel:

 

Der Fehler  wird nun mit der folgenden Formel berechnet:

 

Für die erste Temperaturdifferenz ergibt sich nun:

 

Heizphase	Temperaturdifferenz in K	Heizphase	Temperaturdifferenz in K
1	15,07 ± 0,05	10	9,96 ± 0,3
2	13,53 ± 0,06	11	9,73 ± 0,3
3	12,47 ± 0,09	12	9,59 ± 0,3
4	11,83 ± 0,11	13	9,54 ± 0,3
5	11,31 ± 0,15	14	9,39 ± 0,30
6	10,89 ± 0,2	15	9,24 ± 0,4
7	10,52 ± 0,2	16	9,19 ± 0,3
8	10,34 ± 0,2	17	9,12 ± 0,30
9	10,19 ± 0,3	18	9,02 ± 0,4

^{Tabelle 1: Temperaturdifferenz der einzelnen Heizphasen}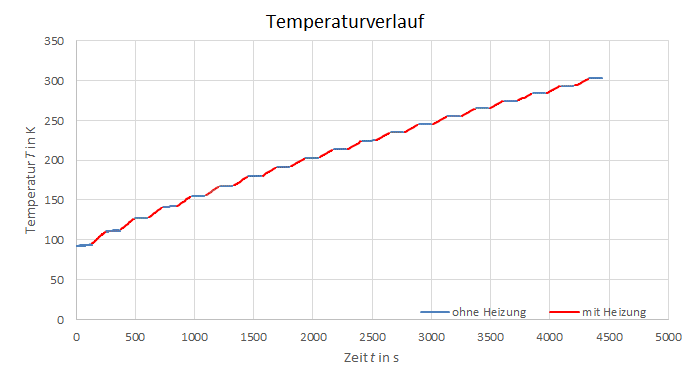

^{Abbildung 2: Temperaturverlauf}

^{Abbildung 3: Umrechnung von R nach T}

 

2.2. Zugeführte Energie pro Heizschritt

 

Heizschritt	Strom in A	Spannung in V	Energie in Ws=J
1	1,290 ± 0,001	198,0 ± 0,1	30650 ± 140
2	1,290 ± 0,001	197,8 ± 0,8	30600 ± 300
3	1,284 ± 0,006	197,0 ± 0,1	30300 ± 300
4	1,280 ± 0,001	197,3 ± 0,8	30300 ± 300
5	1,2813 ± 0,009	197,0 ± 0,1	30300 ± 400
6	1,280 ± 0,001	197,0 ± 0,1	30260 ± 140
7	1,280 ± 0,001	196,5 ± 0,5	30200 ± 200
8	1,275 ± 0,005	196,3 ± 0,8	30000 ± 300
9	1,279 ± 0,001	196,9 ± 0,9	30200 ± 300
10	1,279 ± 0,001	196,8 ± 0,8	30200 ± 300
11	1,275 ± 0,005	196,3 ± 0,8	30000 ± 400
12	1,275 ± 0,005	196,5 ± 0,5	3010 ± 300
13	1,280 ± 0,001	197,0 ± 0,1	30260 ± 140
14	1,275 ± 0,005	197,0 ± 0,1	30100 ± 300
15	1,270 ± 0,001	196,0 ± 0,1	29870 ± 140
16	1,270 ± 0,001	196,0 ± 0,1	29870 ± 140
17	1,270 ± 0,001	196,9 ± 0,9	30000 ± 300
18	1,270 ± 0,001	196,0 ± 0,1	29870 ± 140

Aufgrund der sehr geringen Schwankung der Messwerte für Strom und Spannung und unter Berücksichtigung der Messunsicherheiten, ist es hier ausreichend die Mittelwerte der entsprechenden physikalischen Größen zu bilden und anzunehmen, dass dieser der konstante Wert für die jeweilige Größe ist. Gebildet wird der Mittelwert mit (2.2.1). Anschließend werden die errechneten Mittelwerte in die Gleichung (1.1.2) eingesetzt, um so die insgesamt zugeführte Menge an Energie zu ermitteln. Die für den jeweiligen Mittelwert und der zugeführten Energiemenge je Heizschritt berechneten und gerundeten Werte, können der rechten Tabelle entnommen werden.

 

Fehlerrechnung:

Wir verwenden die Regeln der Fehlerrechnung für Produkte und Quotienten von fehlerhaften Größen, wobei dx der Gesamtfehler von x ist:

 

Für  gilt

       (2.2.2)

und für   gilt

   (2.2.3)

Der Gesamtfehler wird dabei durch die Zusammenrechnung des ermittelten Messfehlers mit der Messunsicherheit der Messgeräte:

                        (2.2.4

Setzt man nun die Gleichung (1.1.2) als  ein, bekommt man die folgende Formel:

     (2.2.5)

Diese Gleichung verwendet man nun für alle Heizschritte und erhält der in der Tabelle 1 angegebenen und bereits gerundeten Unsicherheit der berechneten Energie pro Heizschritt.

Beispielsrechnung für den zweiten Heizschritt:

 

Die restlichen Fehler können der Tabelle entnommen werden.

 

2.3. Spezifische Wärmekapazität

 

 Zur Berechnung der spezifischen Wärmekapazität wird die Gleichung (1.5.1) verwendet. Dabei ist die Masse m des Kupferblocks (8,375 ±0,004) kg, die Wärme Q die in 2.2 berechnete Energie und  die jeweils mittlere Temperatur des jeweiligen Heizschrittes.

Heizschritt	Spezifische Wärmekapazität in
1	243 ± 2
2	270± 4
3	291 ± 5
4	306 ± 6
5	320 ± 8
6	332 ± 8
7	343 ± 10
8	347 ± 12
9	354 ± 13
10	362 ± 13
11	368± 15
12	374 ± 16
13	379 ± 15
14	383 ± 16
15	386 ± 18
16	388 ± 16
17	393 ± 17
18	395 ± 19

^{Tabelle 3: Spezifische Wärmekapazität pro Heizschritt}

Daraus folgt dann:

 

Diese Formel wird dann für jeden Heizschritt verwendet und die gerundeten Ergebnisse können der rechten Tabelle entnommen werden.

 

Fehlerrechnung:

Die Fehlerrechnung erfolgt hier auf die gleiche Art wie bereits in 2.2:

 

Dies erfolgt ebenfalls für jeden einzelnen Heizschritt und die jeweiligen Abweichungen können ebenfalls aus der rechten Tabelle entnommen werden.

 

2.4. Molare Wärmekapazität

 

Zur Berechnung der molaren Wärmekapazität muss zuerst die Stoffmenge n errechnet werden, dies erfolgt mit (1.4.2):

 

Nun wird dieser Wert für die Stoffmenge in die Gleichung (1.5.2) eingesetzt und es folgt:

Dies wird nun erneut für jeden Heizschritt wiederholt und man enthält die gerundeten Werte, welche in Tabelle drei enthalten sind.

^{Abbildung 4: Molare Wärmekapazität als Funktion der Temperatur}

Fehlerrechnung:

Die Fehlerrechnung erfolgt erneut wie in 2.2. Zuerst für die Stoffmenge

 

und anschließend für die molare Wärmekapazität:

Heizschritt	Molare Wärmekapazität in
1	15,43 ± 0,13
2	17,2 ± 0,2
3	18,5 ± 0,3
4	19,4 ± 0,4
5	20,3 ± 0,5
6	21,1 ± 0,5
7	21,8 ± 0,6
8	22,0 ± 0,8
9	22,5 ± 0,8
10	23,0 ± 0,8
11	23,4 ± 0,9
12	23,8 ± 1,0
13	24,1 ± 0,9
14	24,4 ± 1,0
15	24,5 ± 1,1
16	24,7 ± 1,0
17	25,0 ± 1,1
18	25,1 ± 1,2

Die gerundeten Abweichungen der einzelnen molaren Wärmekapazitäten können der Tabelle drei entnommen werden. Des Weiteren kann man nun noch die Molare Wärmekapazität durch die Gaskonstante R teilen. Mit steigenden Temperaturen sollte sich dieser Wert dann dem dreifachen Wert für R annähern.

3. Diskussion

 

Der in Tabelle 3 bestimmte Wert für die spezifische Wärmekapazität von

 bei 29,6 °C

weicht nicht signifikant vom Literaturwert (Tipler) ab:

 bei 20°C und 1 atm

Die Abweichung bei niedrigen Temperaturen lassen sich damit erklären, dass noch nicht alle Freiheitsgrade aktiv sind, es aber mit zunehmender Temperatur mehr werden. Mit den letzten Heizschritten nähern sich die Werte für Kupfer, mit 345 K, und der maximalen molaren Wärmekapazität von

 

gut an. Die Aufnahme weiterer Wertepaare und kürzere Messzeitabstände, würde die Fehlerabweichung verringern und die Präzision der Berechnungen verbessern.                             Weiterhin beeinflusst die menschliche Reaktionszeit die exakte Dokumentation der Daten erheblich. Eine automatische Erfassung der gemessenen Werte, in bestimmten Intervallen, würde die Messungenauigkeit deshalb deutlich verbessern. Außerdem könnte man die Kiste besser isolieren, da auch ohne Heizung bei den einzelnen Phasen Anstiege von über 1 K zu beobachten sind. Des Weiteren könnte man, sofern es der Versuchsaufbau zulässt, die Temperatur noch weiter erhöhen um noch mehr Werte aufnehmen zu können. Auch die Fehler durch Näherungsgleichungen könnten reduziert werden, indem man z.B. alle Widerstände direkt von der Widerstandstabelle in Temperaturen umrechnet.

 

4. Zusammenfassung

 

Die ermittelten Werte für die spezifische und molare Wärmekapazität von Kupfer liegen bei:

 bei 29,6 °C