Praktikumsprotokoll Luftfeuchtigkeit und Taupunkt

Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.

Luftfeuchtigkeit und Taupunkt

Inhaltsverzeichnis

Abbildungsverzeichnis

Tabellenverzeichnis

1. Grundlagen

1.1. Ideale und reale Gase

1.2. Sättigungsdampfdruck und das Daltonsche Gesetz

1.3. p-V-Diagramme

1.4. Absolute und relative Luftfeuchtigkeit

1.5. Thermoelement, Peltierelement und Zusammensetzung der Luft

2. Auswertung

2.1. Normale Luftfeuchtigkeit

2.1.1. Bestimmung der Taupunkt-Temperatur

2.1.2. Berechnung der absoluten Luftfeuchtigkeit

2.1.3. Beitrag des Wasserdampfes zum Luftdruck

2.1.4. Berechnung der relativen Luftfeuchtigkeit

2.2. Erhöhte Luftfeuchtigkeit

3. Diskussion

3.1. Diskussion und Vergleich mit Literaturwerten

3.2. Verbesserungsmöglichkeiten

4. Zusammenfassung

Quellenverzeichnis

Messprotokoll

Abbildungsverzeichnis

Abbildung 1: Absolute Luftfeuchtigkeit über Zeit

Abbildung 2: Absolute Luftfeuchtigkeit über Zeit

Tabellenverzeichnis

Tabelle 1: Messwerte und Taupunkt-Temperatur

Tabelle 2: Taupunkt-Temperatur und absolute Luftfeuchtigkeit

Tabelle 3: Beitrag des Wasserdampfes zum Luftdruck

Tabelle 4: Dampfdruck und relative Luftfeuchtigkeit

Tabelle 5: Berechnete Messwerte für erhöhte Luftfeuchtigkeit

Tabelle 6: Gemittelte Messwerte

1. Grundlagen

1.1. Ideale und reale Gase

Ein idealisiertes Gas ist eine Vereinfachung von einem realen Gas, um dieses Gas einfacher berechnen zu können. Es existieren dabei primär drei große Unterschiede zwischen den Gasen. Bei einem idealisierten Gas werden alle Gasteilchen als Massepunkte ohne Ausdehnung angenommen und die Stöße untereinander, beziehungsweise zwischen den Wänden des Gasbehälters sind immer ideal elastische Stoßvorgänge. Weiterhin wird der mittlere Abstand zwischen den Teilchen als sehr viel größer als der Teilchendurchmesser angenommen. Über diese Eigenschaften verfügen reale Gase normalerweise nicht, allerdings lässt es sich mit diesen Vereinfachung deutlich leichter rechnen und die Ergebnisse sind für die weitere Verwendung meistens präzise genug. Berechnet werden sie mit den folgenden Zustandsgleichungen:

   (1.1.1)

Dabei steht p für den Druck, V für das Volumen, n die Stoffmenge, R die universelle Gaskonstante, T für die Temperatur in Kelvin, m die Masse des Gases, N für die Teilchenzahl,  für die spezifische Gaskonstante und  für die Boltzmann-Konstante. Wie bereits erwähnt verfügen reale Gase normalerweise nicht über diese Eigenschaften von idealen Gasen. Wenn man von ihnen allerdings nur eine niedrige Konzentration hat und diese auf eine hohe Temperatur erhitzt, dann verhalten sie sich auch wie ein ideales Gas. Das liegt daran, dass der mittlere Abstand dann deutlich größer als der Teilchendurchmesser, die kinetische Energie deutlich größer als die Bindungsenergie ist und die Stoßkräfte deutlich größer als die Anziehungskräfte sind. Die realen Gase können mit der Van-der-Waals-Zustandsgleichung ebenfalls näherungsweise berechnet werden. Die Gleichung lautet:

             (1.1.2)

 steht dabei für das molare Volumen, a für den Kohäsionsdruck und b für das Kovolumen, wobei a und b materialabhängige Werte sind.

1.2. Sättigungsdampfdruck und das Daltonsche Gesetz

Das Daltonsche Gesetz besagt, dass sich der Gesamtdruck eines Gasgemisches aus dem Partialdruck jedes Gases zusammensetzt. Der Partialdruck entspricht dabei dem Druck, den jedes Gas hätte, wenn es nur alleine in dem betreffenden Volumen vorhanden wäre. Die Gleichung dazu lautet:

Das Gesetz ist allerdings nur eine Näherung, da es für ideale Gase gedacht ist. Der Sättigungsdampfdruck ist der Punkt, bei dem sich der gasförmige Zustand in einem Gleichgewicht mit dem flüssigen Zustand befindet. Es würden also genau so viele Gasmoleküle in die Flüssigkeit übergehen, wie Flüssigkeitsmoleküle in das Gas wandern. Wo genau dieser Punkt liegt, ist von der aktuell herrschenden Temperatur abhängig.

1.3. p-V-Diagramme

Isotherme werden in der Thermodynamik verwendet, um das Verhältnis des Volumens und des Drucks, bei konstanter Temperatur, abzubilden. Errechnet werden die jeweiligen Linien, in dem man die Gleichung:

      (1.4.1)

verwendet. Ein noch erwähnenswerter Sonderfall, ist der sogenannte kritische Punkt. Bei diesem Punkt im pV-Diagramm stimmen, bei einem realen Gas, die Eigenschaften für gasförmig und flüssig überein. Das heißt, es existiert kein Unterschied mehr zwischen Flüssigkeit und Dampf. Dieser Punkt befindet sich exakt da, wo der Gasdruck  und der Flüssigkeitendruck  genau übereinstimmen.

1.4. Absolute und relative Luftfeuchtigkeit

Die absolute Luftfeuchtigkeit  gibt das maximale Aufnahmevermögen von Luft an, also wieviel Wasserdampf es bei einer bestimmten Temperatur aufnehmen kann. Dabei gilt, je höher die Temperatur, desto mehr kann sie aufnehmen und je niedriger, desto weniger kann sie aufnehmen. Die aufgenommene Dampfmenge wird dabei in  angegeben und berechnet mit der Gleichung:

Dabei ist  der partielle Wasserdampfdruck,  die Wassermolekülmasse und  die Taupunkttemperatur. Wobei die Taupunkttemperatur genau die Temperatur ist, bei der sich die Luft soweit herunter gekühlt hat, dass sie den Wasserdampf nicht mehr halten kann und sich das überschüssige Wasser als Tau niederschlägt. Die relative Luftfeuchtigkeit  hingegen gibt an, wieviel Prozent der maximal aufnehmbaren Feuchtigkeit in der Luft enthalten ist. Sie ist dabei, genau wie die absolute Luftfeuchtigkeit, von der Temperatur abhängig. Dadurch ist es dann auch möglich, dass Luft mit einer relativen Luftfeuchtigkeit von 70 % weniger Wasserdampf enthält, als eine heißere Luft mit einer relativen Luftfeuchtigkeit von nur 50 %. Berechnet wird sie mit der Gleichung:

Dabei ist  der Sättigungsdampfdruck.

1.5. Thermoelement, Peltierelement und Zusammensetzung der Luft

Die Luft setzt sich im Wesentlichen aus den Gasen Stickstoff (), Sauerstoff () und Argon () zusammen. Sie enthält aber auch noch circa 20 weitere Gase, welche allerdings nur in geringen Mengen enthalten sind. Das Thermoelement ist ein Messgerät, welches eine Spannung aus einer Temperaturdifferenz erzeugen kann. Es besteht hauptsächlich aus zwei Leitern, welche jeweils aus unterschiedlichen, leitenden, Materialien bestehen und zusammen gelötet sind. Aufgrund der unterschiedlichen Potentiale der Leitern, kommt es an den Lötstellen zu einer Kontaktspannung. Setzt man nun das Thermoelement einem Temperaturgefälle aus, dann entsteht dadurch eine Thermodiffusion. Dies ist eine, durch die Temperaturdifferenz der beiden Kontaktstellen, ausgelöste Verschiebung der Ladung. Dadurch lädt sich der kältere Leiter negativ auf und es entsteht eine Thermospannung. Da nun auch ein Spannungsmessgerät, mit einem hohen elektrischen Wiederstand, angeschlossen ist, kann es auch nicht zu einem Kreisstrom kommen, welcher hier nun normalerweise entstehen würde. Deswegen kann das Thermoelement als ein Temperaturmessgerät verwendet werden. Das Peltierelement hingegen nutzt den gleichen Effekt wie das Thermoelement, allerdings anders herum und kann so eine Temperaturdifferenz aus einer anliegenden Spannung erzeugen.

2. Auswertung

2.1. Normale Luftfeuchtigkeit

2.1.1. Bestimmung der Taupunkt-Temperatur

Die Taupunkt-Temperatur wird mit  berechnet, wobei  die Lufttemperatur und  die Thermospannung ist. Zur Bestimmung der Taupunkt-Temperatur wurden Lufttemperatur und Thermospannung bei Beschlagen des Spiegels mehrmals gemessen, verwendet wurden dazu ein Thermometer () und  ein Voltcraft Plus VC920 Voltmeter (). Für das erste Wertepaar ergibt sich:

Der Fehler ist von den gemessenen Werten unabhängig und somit gleich für die gesamte Messreihe:

2.1.2. Berechnung der absoluten Luftfeuchtigkeit

Die absolute Luftfeuchtigkeit wird berechnet mit der Formel:

             (2.1.2.1)

, wobei die Masse der Wassermoleküle , die Boltzmann Konstante  und  der Partialdruck des Wasserdampfes ist, welcher aus der Dampfdrucktabelle abgelesen werden kann. Für den ersten Wert der Taupunkt-Temperatur erhält man so:

^{Tabelle 2: Taupunkt-Temperatur und absolute Luftfeuchtigkeit}

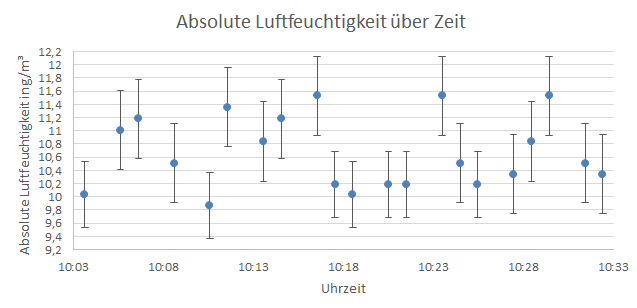
 Trägt man nun die für die absolute Luftfeuchtigkeit berechneten Werte über die Uhrzeit auf, erhält man folgendes Diagramm:

^{Abbildung 1: Absolute Luftfeuchtigkeit über Zeit}

Anhand des Diagramms erkennt man, dass es Schwankungen in der absoluten Luftfeuchtigkeit gab, welche wahrscheinlich dadurch verursacht wurden, dass während des Versuchs das Fenster geöffnet, sowie die Tür mehrmals geöffnet und geschlossen wurde. Außerdem wurde im selben Raum für einen anderen Versuch Wasser gekocht, wodurch sich zusätzlicher Wasserdampf in der Luft befand.

2.1.3. Beitrag des Wasserdampfes zum Luftdruck

Der Beitrag des Wasserdampfes zum Luftdruck wird berechnet durch:

        (2.1.3.1)

, wobei  der Luftdruck ist. Der Luftdruck wurde mit einem Barometer zu   gemessen.

Für den ersten Messwert ergibt sich:

2.1.4. Berechnung der relativen Luftfeuchtigkeit

Die relative Luftfeuchtigkeit wird berechnet mit:

     (2.1.4.1)

, wobei  der (Sättigungs-) Dampfdruck bei aktueller Temperatur ist, und ebenfalls aus der Dampfdrucktabelle abgelesen wird. Für die ersten Messwerte ergibt sich:

2.2. Erhöhte Luftfeuchtigkeit

Alle Rechnungen erfolgen genauso, wie bei normaler Luftfeuchtigkeit.

Trägt man nun wieder die absolute Luftfeuchtigkeit über die Uhrzeit auf erhält man dieses Diagramm:

^{Abbildung 2: Absolute Luftfeuchtigkeit über Zeit}

Auch hier sind wie bei der normalen Luftfeuchtigkeit Schwankungen zu beobachten, welche durch dieselben Störfaktoren zu erklären sind. Außerdem war es bei dem Blick durch die Plexiglashaube schwerer zu beurteilen, wann der Spiegel anfing zu beschlagen, was einen größeren statistischen Fehler zur Folge gehabt haben könnte.

3. Diskussion

3.1. Diskussion und Vergleich mit Literaturwerten

Nun werden für die jeweiligen Messgrößen noch Mittelwerte gebildet:

Bei normaler Luftfeuchtigkeit liegt die Taupunkt-Temperatur, wenn man die Toleranzen berücksichtigt, mit der hier bestimmten Raumtemperatur und relativen Luftfeuchtigkeit nach den Literaturwerten [2] zwischen 4,5 °C und 8,5 °C, und weicht somit nicht signifikant von der im Versuch bestimmten Taupunkt-Temperatur ab. Für die erhöhte Luftfeuchtigkeit liegen die Literaturwerte zwischen 8,7 °C und 15,3 °C und weichen ebenfalls nicht signifikant von den bestimmten Werten ab. Bei normaler Luftfeuchtigkeit liegt nach [6] mit den hier bestimmten Werten die absolute Luftfeuchtigkeit zwischen 5,2  und 9,2 , für erhöhte Luftfeuchtigkeit zwischen 6,9  und 13,8 , auch hier weichen beide Werte nicht signifikant von den im Versuch bestimmten Werten ab.

3.2. Verbesserungsmöglichkeiten

Um präzisere Messergebnisse erzielen zu können, wäre es besser, wenn der Versuch in einem Raum stattfinden würde, in dem Lufttemperatur und Wasserdampfmenge in der Luft gleichbleiben sind und nicht durch andere Versuche beeinflusst werden. Außerdem könnte ein optischer Sensor verwendet werden um zu bestimmen, wann der Spiegel beschlägt, da dies sonst eine subjektive Einschätzung des Protokollanten ist.

4. Zusammenfassung

Die in diesem Versuch für normale Luftfeuchtigkeit bestimmten Werte liegen für bei:

Für erhöhte Luftfeuchtigkeit bei  liegen sie bei:

Quellenverzeichnis

1. Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
2. Erfurt. (kein Datum). Abgerufen am 18. Oktober 2014 von Erfurt: http://www.erfurt.com/cms/fileadmin/Bildarchiv/Sonstiges/ES_Tabelle_Taup...
3. Meschede, D. (2010). Gerthsen Physik (24. überarbeitete Ausg.). Springer-Verlag.
4. Schmucker, M., Reinlein, O., & Hensel, C. (kein Datum). Universität Bayreuth. Abgerufen am 16. September 2014 von Universität Bayreuth: http://daten.didaktikchemie.uni-bayreuth.de/umat/gas_real/gas_real.htm
5. Tipler, P. A. (2000). Physik (3. korrigierte Ausg.). Spektrum Akademischer Verlag.
6. Transport-Information-Service. (kein Datum). Abgerufen am 11. Oktober 2014 von Transport-Information-Service: http://www.tis-gdv.de/tis/misc/klima.htm
7. Universität Ulm. (kein Datum). Abgerufen am 30. September 2014 von Universität Ulm: http://www.uni-ulm.de/mp-physik/Physik%20I/zusammen_4.4/ideales_reales_G...
8. Wikipedia - Die freie Enzyklopädie. (kein Datum). Abgerufen am 7. Oktober 2014 von Wikipedia - Die freie Enzyklopädie: http://de.wikipedia.org/wiki/P-T-Diagramm