Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Erzwungene Schwingungen
Inhaltsverzeichnis
1.1. Gedämpfte harmonische Schwingungsdifferentialgleichungen
1.2. Erzwungene, gedämpfte harmonische Schwingungsdifferentialgleichungen
1.3. Amplitude und Phasenverschiebung
2.1. Bestimmung der Schwingungsdauer T
2.3. Amplitudenmessung in Abhängigkeit der anregenden Frequenz
3.1. Diskussion und Vergleich mit Literaturwerten
Tabelle 1: Messwerte Versuch 1
Tabelle 2: Messwerte Versuch 2
Tabelle 3: Dämpfungsdekremente
Tabelle 4: Messwerte Versuch 3
1.1. Gedämpfte harmonische Schwingungsdifferentialgleichungen
Durch die Auslenkung eines Systems, welches sich im Gleichgewicht befindet, entsteht eine gedämpfte harmonische Schwingung. Die Schwingungsdifferentialgleichung für eine gedämpfte harmonische Drehschwingung lautet:
(1.1.1)
Wobei der Momentanbeschleunigung, der Momentangeschwindigkeit, y der Auslenkung, der Eigenfrequenz der gedämpften Schwingung und dem Abklingkoeffizienten entspricht. setzt sich dabei zusammen aus D, dem Dämpfungsmaß, und . Die während der Bewegung auftretende Reibung wirkt der Schwingung entgegen und bremst sie so immer weiter ab, bis sie schließlich vollständig zum Erliegen kommt. Die Schwingungsenergie wird dabei an die Umgebung übertragen. Die Zeit, welche bis zum Erliegen der Schwingung, benötigt wird, ist maßgeblich von der Art der gedämpften Schwingungen abhängig. Es wird dabei zwischen den drei nun folgenden Schwingungsarten unterschieden. Bei dem ersten Fall, dem Schwingfall, entsteht, aufgrund einer geringer Dämpfung (), eine lange Schwingdauer und die Wiederherstellung des ursprünglichen Systemgleichgewichts stellt sich erst nach einem längeren Zeitraum wieder ein. Dem entgegen steht der zweite Fall, der Kriechfall, bei dem eine starke Dämpfung existiert (), weshalb das ausgelenkte System hier nur vergleichsweiße kurz schwingt, bis sich die Gleichgewichtslage wieder einstellt. Der dritte und auch letzte Fall, der aperiodische Grenzfall, stellt die schnellste Variante des Kriechfalls dar. Bei diesem erfolgt, aufgrund der Dämpfungsart (), fast überhaupt keine Schwingung wenn das System ausgelenkt wird und es kommt zu eine sehr schnelle Wiederherstellung des anfänglichen Gleichgewichts.
1.2. Erzwungene, gedämpfte harmonische Schwingungsdifferentialgleichungen
Die Schwingungsdifferentialgleichung für eine erzwungene, gedämpfte harmonische Drehschwingung lautet:
(1.2.1)
wobei ist. M ist dabei das antreibende, äußere Drehmoment und J das Trägheitsmoment des starren Körpers. Durch die äußere Krafteinwirkung wird das Gleichgewicht des Systems gestört und es entsteht eine Schwingung. Aufgrund der Dämpfung wird die Schwingung, wie bei der ungezwungenen Schwingung, mit der Zeit immer geringer. Da allerdings die äußere Kraft weiterhin einwirkt, stellt sich ab einem gewissen Zeitpunkt die Schwingung eben jener Kraft ein und es entsteht der stationäre Zustand. Dabei gilt, je stärker die Dämpfung, desto schneller wird dieser Zustand erreicht.
1.3. Amplitude und Phasenverschiebung
Eine erzwungene Schwingung ist abhängig von der Amplitude der antreibenden Kraft und deren Frequenz. Je nachdem wie groß diese beiden Werte sind und die ebenfalls auftretende Reibung ist, stellt sich schließlich das neue Gleichgewicht ein. Die dabei entstehenden Resonanzkurven, sind größer je kleiner die Dämpfung und kleiner desto größer die Dämpfung wird. Die Formel zu ihrer Berechnung lautet:
. (1.3.1)
Wobei für die Breite der Resonanz steht. Die Phasendifferenz zwischen der erzwungenen Schwingung und der Anregung ist von der Erregerfrequenz abhängig. Bei einem ungedämpften Fall springt sie von 0 auf π. Mit steigender Dämpfung verlangsamt sich dieser Sprung immer weiter und die Kurve nähert sich mehr und mehr einer Geraden an.
2.1. Bestimmung der Schwingungsdauer T
|
Messwert in s |
|
|
1 |
19,1 ± 0,2 |
|
2 |
19,4 ± 0,2 |
|
3 |
19,4 ± 0,2 |
|
4 |
19,2 ± 0,2 |
|
5 |
19,3 ± 0,2 |
|
6 |
19,2 ± 0,2 |
|
7 |
19,4 ± 0,2 |
|
8 |
19,2 ± 0,2 |
|
9 |
19,3 ± 0,2 |
|
10 |
19,3 ± 0,2 |
Tabelle 1: Messwerte Versuch 1
Um die Zeit für die zehn Schwingungen zu messen, wurde eine Stoppuhr mit zwei Nachkommastellen verwendet. Die damit ermittelten Messerwerte können der rechts abgebildeten Tabelle entnommen werden. Die, durch das menschliche Reaktionsvermögen und Ungenauigkeit der Stoppuhr, angenommene Messungenauigkeit liegt bei ± 0,2 s. Für die Mittelwertberechnung gilt die Formel:
. (2.1.1)
Durch Einsetzen der ermittelten Messwerte ergibt sich daraus ein Mittelwert von s. Die genaue Bestimmung der Standardabweichung σ erfolgt dann mittels der Formel und ergibt 0,1 s. Die Standardabweichung des Mittelwertes wird nun berechnet durch s. Das Ergebnis, auf der Grundlage der zehn erfolgten Messungen, liegt damit bei s. Teilt man diesen Wert nun durch zehn, dann erhält man die Schwingungsdauer s.
|
Anfangsauslenkung in skt |
Maximale Auslenkung der 5. Schwingung in skt |
|
|
0,1 A Messung 1 |
10,8 ± 0,05 |
9,4 ± 0,3 |
|
0,1 A Messung 2 |
9,8 ± 0,05 |
8,0 ± 0,3 |
|
0,1 A Messung 3 |
8,8 ± 0,05 |
7,3 ± 0,3 |
|
0,1 A Messung 4 |
7,8 ± 0,05 |
6,4 ± 0,3 |
|
0,1 A Messung 5 |
6,8 ± 0,05 |
5,2 ± 0,3 |
|
0,2 A Messung 1 |
10,8 ± 0,05 |
6,4 ± 0,3 |
|
0,2 A Messung 2 |
9,8 ± 0,05 |
5,6 ± 0,3 |
|
0,2 A Messung 3 |
8,8 ± 0,05 |
5,0 ± 0,3 |
|
0,2 A Messung 4 |
7,8 ± 0,05 |
4,3 ± 0,3 |
|
0,2 A Messung 5 |
6,8 ± 0,05 |
3,7 ± 0,3 |
|
0,4 A Messung 1 |
10,8 ± 0,05 |
1,6 ± 0,3 |
|
0,4 A Messung 2 |
9,8 ± 0,05 |
1,5 ± 0,3 |
|
0,4 A Messung 3 |
8,8 ± 0,05 |
1,3 ± 0,3 |
|
0,4 A Messung 4 |
7,8 ± 0,05 |
1,0 ± 0,3 |
|
0,4 A Messung 5 |
6,8 ± 0,05 |
0,9 ± 0,3 |
Tabelle 2: Messwerte Versuch 2
Zur Messung der Stromstärke wurde ein PeakTech 2005, mit einer Messungenauigkeit von ± 0,01 A, verwendet und die Auslenkungsmessung erfolgte per Augenmaß, wofür eine Ungenauigkeit von ± 0,3 skt angenommen wird, aufgrund der manuellen Auslenkung, wird die Unsicherheit für die Anfangsauslenkung auf geschätzt. Die ermittelten Messwerte können der Tabelle 2 entnommen werden, welche bereits den Nullpunkt von 0,8 skt berücksichtigt. Für die Berechnung des logarithmischen Dämpfungsdekrements gilt:
(2.2.1)
für , wobei die maximale Auslenkung der i-ten Schwingung ist. Setzt man nun bspw. das erste Wertepaar aus Tabelle 2 ein, so erhalten wir:
|
für Messwerte |
|
|
0,1 A Messung |
0,035 ± 0,009 |
|
0,051 ± 0,011 |
|
|
0,047 ± 0,012 |
|
|
0,049 ± 0,013 |
|
|
0,067 ± 0,016 |
|
|
0,2 A Messung |
0,131 ± 0,013 |
|
0,140 ± 0,015 |
|
|
0,141 ± 0,016 |
|
|
0,149 ± 0,019 |
|
|
0,152 ± 0,022 |
|
|
0,4 A Messung |
0,48 ± 0,05 |
|
0,47 ± 0,05 |
|
|
0,48 ± 0,06 |
|
|
0,51 ± 0,08 |
|
|
0,51 ± 0,09 |
Tabelle 3: Dämpfungsdekremente
Alle anderen Werte für die Dämpfungsdekremente können Tabelle 3 entnommen werden. Die Mittelwerte für Λ werden nun mittels (2.1.1) berechnet:
Für die jeweilige Messreihe ergibt sich nun der Fehler des Mittelwerts aus der größten Differenz zwischen Mittelwert und Messwert, sowie dem größten berechneten Fehler für der jeweiligen Messreihe. Für die Messreihe mit ergibt sich dann:
Daraus ergeben sich nun folgende Messwerte für :
Außerdem gilt noch:
(2.2.2)
wobei die Dämpfungskonstante ist. Verwenden wir nun die zuvor berechneten Werte für so erhalten wir:
Nun müssen noch die Fehler für die jeweiligen Werte ermittelt werden. Dies erfolgt mit der Gleichung:
(2.2.3)
2.3. Amplitudenmessung in Abhängigkeit der anregenden Frequenz
Zur Messung der Stromstärke wurde wieder das PeakTech 2005, zur Zeitmessung erneut die Stoppuhr aus Versuch 1 verwendet und die Auslenkungsmessung erfolgte per Augenmaß. Die dadurch erhaltenen Messwerte können der nächsten Tabelle 4 entnommen werden, welche bereits den Nullpunkt von 0,8 skt und die Berechnung einer einzigen Schwingungsdauer T berücksichtigt. Basierend auf diesen Messdaten wurden anschließend die Resonanzkurven, siehe Abbildung 6, aufgetragen, wobei die aufgetragene Frequenz f mit der Gleichung:
(2.3.1)
|
0,1 A in skt |
0,2 A in skt |
0,4 A in skt |
|
|
1,30 ± 0,04 |
0,7 ± 0,2 |
0,6 ± 0,2 |
0,6 ± 0,2 |
|
1,52 ± 0,04 |
1,0 ± 0,2 |
0,9 ± 0,2 |
0,8 ± 0,2 |
|
1,66 ± 0,04 |
1,6 ± 0,2 |
1,5 ± 0,2 |
1,3 ± 0,2 |
|
1,88 ± 0,04 |
5,3 ± 0,2 |
4,8 ± 0,2 |
2,8 ± 0,2 |
|
1,90 ± 0,04 |
14,0 ± 0,2 |
9,2 ± 0,2 |
2,9 ± 0,2 |
|
1,92 ± 0,04 |
19,8 ± 0,2 |
10,2 ± 0,2 |
3,0 ± 0,2 |
|
1,98 ± 0,04 |
7,8 ± 0,2 |
3,2 ± 0,2 |
2,8 ± 0,2 |
|
2,06 ± 0,04 |
2,8 ± 0,2 |
2,4 ± 0,2 |
2,0 ± 0,2 |
|
2,27 ± 0,04 |
2,0 ± 0,2 |
1,8 ± 0,2 |
1,6 ± 0,2 |
|
2,48 ± 0,04 |
1,4 ± 0,2 |
1,3 ± 0,2 |
1,2 ± 0,2 |
Tabelle 4: Messwerte Versuch 3
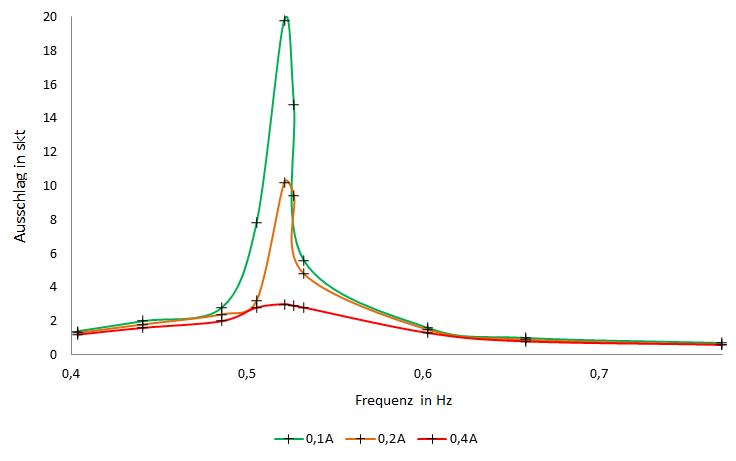
berechnet wurde. Es wird daraus ersichtlich, dass die Amplitude am größten wird, wenn die anregende Frequenz der Eigenfrequenz entspricht, wie bereits in den Grundlagen, unter Punkt 1.4, beschrieben.
Abbildung 1: Resonanzkurven
3.1. Diskussion und Vergleich mit Literaturwerten
Die bei Versuch 1, von dem ermittelten Fehlerwert von für je 10 T, abweichenden Messwerte lassen sich auf die menschliche Reaktionszeit und die, aufgrund der schnellen Bewegung, nur ungenau ablesbaren Skalenanzeige zurückführen. Eine nennenswerte Verfälschung durch weitere unentdeckte systematische Fehler ist unwahrscheinlich. Die Abweichungen bei Versuch 2 lassen sich auf die menschliche Reaktionszeit und die, aufgrund der schnellen Bewegung, nur ungenau ablesbaren Skalenanzeige zurückführen. Eine nennenswerte Verfälschung durch weitere unentdeckte systematische Fehler ist unwahrscheinlich.
3.2. Verbesserungsmöglichkeiten
Aufgrund der menschliche Reaktionszeit und der Tatsache, dass die Skalenanzeige, aufgrund der schnellen Bewegung, nur ungenau ablesbare ist, werden die Messergebnis deutlich beeinflusst. Eine Verbesserungsmöglichkeit wäre hier die Verwendung einer Hochgeschwindigkeitskamera um den maximalen Ausschlag exakt ablesen zu können. Weiterhin könnte bei Versuch 1 eine Lichtschranke verwendet werden, um eine präzisere Schwingungsdauer T zu ermitteln. Des Weiteren würde die Verwendung eines Motors mit einer direkten Anzeige seiner Schwingungsdauer, genauere Messdaten liefern. Außerdem wäre die Aufnahme weiterer Wertepaare eine zusätzliche Möglichkeit, um die Berechnung eines möglichst genauen Mittelwertes und der dazugehörigen Standardabweichung zu verbessern.
Bei diesem Versuch wurde die Schwingungsdauer T eines Drehpendels ohne elektromagnetische Dämpfung zu folgendem Wert bestimmt:
s
Weiterhin wurde die Amplitude eines Pendels mit unterschiedlichen Dämpfungen gemessen und die Dämpfungskonstante bestimmt. Die Ergebnisse sind:
Und zuletzt wurde noch die Amplitude, in Abhängigkeit einer anregenden Frequenz und unterschiedlichen Dämpfungen, gemessen und für jede Dämpfung eine Resonanzkurve, siehe Abbildung 6, aufgetragen. Dabei lag die Resonanzfrequenz bei (0,52 ± 0,01) Hz.
- Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
- Erdmann, M. (2011). Physik Denken - Exprimentalphysik 3 - Schwingungen, Wellen, Körperdrehungen (1. Ausg.). Springer-Verlag.
- Goertz, S. (kein Datum). Universität Bonn. Abgerufen am 2. September 2014 von Universität Bonn: http://pi.physik.uni-bonn.de/~goertz/Blockseminar/Versuch6.pdf
- Kraus, D., & Pieper, W. (kein Datum). Hochschule Bremen. Abgerufen am 2. September 2014 von Hochschule Bremen: http://homepages.hs-bremen.de/~krausd/iwss/V5a.pdf
- Tipler, P. A. (2000). Physik (3. korrigierte Ausg.). Spektrum Akademischer Verlag.