You are here
Praktikumsprotokoll Akustischer Festkörper
Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls C-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Akustischer Festkörper
Inhaltsverzeichnis
2.1. Bestimmung der Schallgeschwindigkeit aus den Resonanzfrequenzen
2.3. Bestimmung der Wellenlänge
2.4. Effektive Schallunterdrückung
Abbildung 1: Resonanzfrequenz im leeren Rohr
Abbildung 2: Wellenzahl in Abhängigkeit der Frequenz
Abbildung 3: Resonanzfrequenz mit Hülsen
In diesem Versuch ist es das Ziel, die Resonanzfrequenz eines verschlossenen Rohres, welches einmal leer und einmal mit zwölf Blenden gefüllt ist, zu ermitteln und die akustische Bandlücke zu ermitteln.
Eine Welle ist einfach ausgedrückt, die periodische Ausbreitung einer Schwingung in Raum und Zeit, während die Schwingung selbst nur eine periodische Bewegung eines Körpers um seine eigene Ruhelage ist. Wenn man bei einer Welle allerdings nur einen einzelnen, bestimmten Punkt betrachtet, dann sieht dieser wie eine Schwingung aus. Des Weiteren teilt sich die Welle in zwei unterschiedliche Wellenarten auf. Einmal gibt es die transversale Welle, auch Quer- oder Schubwelle genannt, bei der die Ausbreitung senkrecht zur Schwingung erfolgt. Beispiele dafür wären die Welle entlang eines Seiles oder Licht in einem Vakuum. Die andere Wellenart ist die longitudinale Welle, auch Längswelle genannt, bei der die Ausbreitungsrichtung der Schwingungsrichtung entspricht. Sowas geschieht beispielsweise bei Schallwellen in Gasen oder Flüssigkeiten und benötigt also, anders als elektromagnetische Wellen, ein Trägermedium. Mathematisch kann man diese Wellen mit der Wellengleichung erklären:
(1.2.1)
Wobei die Kompressibilität und der Druck p definiert sind durch:
(1.2.2)
(1.2.3)
Dabei ist t die Zeit, das Volumen, R die universelle Gaskonstante, m die Gasmasse, M die Molmassen und p der Druck. Aus Gleichung (1.2.1) folgt dann, das c² gleich:
(1.2.4)
ist. Durch die Lösung der Wellengleichung bekommt man dann die folgende Wellenfunktion:
(1.2.5)
dabei steht für die Auslenkung des Teilchens aus der Ruhelage, für die Amplitude, die Kreisfrequenz, k für die Wellenzahl, x für den Ortsvektor und t für die Zeit. Möchte man nun, beispielsweise wie in diesem Versuch, die Maximalgeschwindigkeit eines Pendels berechnen, verwendet man die Schwingungsgleichung:
(1.2.6)
bei der A für die Amplitude, für die Winkelgeschwindigkeit und für die Phase steht. Die Winkelgeschwindigkeit lässt sich dabei berechnen mittels der Formel:
(1.2.7)
wobei T die Schwingungsdauer darstellt. Setzt man die Gleichung (1.2.7) nun in (1.2.6) ein und leitet sie ab, so erhält man:
(1.2.8)
woraus sich die maximale Geschwindigkeit, welche das Pendel erreichen kann, errechnen lässt. Dazu muss man nur den Cosinus seinen Maximalwert einsetzen, also eins, und erhält so die Formel:
(1.2.9)
Des Weiteren existieren bei Wellen auch so genannte Wellenbäuche und Knoten. Ein Bauch entsteht genau da, wo sich bei einer stehenden Welle die maximale Amplitude befindet. Die Bäuche haben dabei einen Abstand von einer halben Wellenlänge und zwischen ihnen befindet sich immer ein Knoten. Diese Knoten sind, bei einer ebenen Welle, immer da, wo sich die minimale Amplitude einer Welle befindet. In einer zweidimensionalen Umgebung sind es Knotenlinien und in einer dreidimensionalen Knotenebenen. Außerdem verfügen Wellen auch über die Eigenschaft sich, aufgrund des Superpositionsprinzips, sich zu überlagern. Dies bedeutet, dass das aufeinander treffen mehrerer Wellen zur Bildung einer neuen Welle führt. Dabei entspricht deren Auslenkung einer Addition der Einzelauslenkungen der ursprünglichen Wellen. Sollte die Auslenkung der unterschiedlichen Wellen dabei identisch sein, so bildet sich dadurch eine stehende Welle, deren Auslenkung an bestimmten Stellen immer gleich Null ist. Dabei können sich die Wellen durch unterschiedliche Quellen oder durch das reflektieren einer Welle an einer Wand bilden. Die Gesamtlänge l der dadurch erzeugten Wellen lässt sich dabei mit der Gleichung:
(1.2.10)
berechnen, wobei der Wellenlänge entspricht. Die daraus resultierenden Eigenfrequenzen lassen sich dann mittels der Formel:
(1.2.11)
errechnen, wobei c für die Schallgeschwindigkeit, beziehungsweise Phasengeschwindigkeit, steht.
Mit dem Bändermodell ist es möglich, die Leitungsvorgänge innerhalb eines Festkörpers zu beschreiben. Dazu betrachtet man die Atome des Festkörpers und wie sie sich verhalten, wenn sie sich einander annähern. Bei dieser Annäherung beginnen die Energieniveaus der beteiligten Atome, aufgrund der Wechselwirkung untereinander, sich zu verschieben und es wirkt so, als wenn sich das Energieniveau in zwei neue Niveaus mit verschiedenen Energien aufteilen. Dabei ist die Menge an Aufteilungen von der Menge der beteiligten Atome abhängig. Sind also viele Atome vorhanden, wie bei einem Festkörper, dann erfolgt eine Aufspaltung in viele Energieniveaus, welche dicht zusammenliegen und deshalb auch als Band bezeichnet werden. Je nachdem um welche Atom- und Bindungsart es sich dabei handelt, können sich die Bänder im Festkörper überlappen, nahe beieinander liegen oder einen größeren Abstand zueinander haben. Dabei wird das höchste und auch energiereichste Band Valenzband genannt und seine Elektronenbesetzung bestimmt die Leiterart eines Festkörpers. Wenn das Band vollständig mit Elektronen gefüllt ist, dann handelt es sich um einen Isolator oder Nichtleiter. Legt man an diesem nun ein elektrisches Feld an, dann können sich, aufgrund der vollständigen Besetzung aller energetischen Zustände innerhalb des Bandes, keine weiteren Elektronen mehr durch das Band bewegen. Zusätzlich existiert eine Energielücke, welche auch als Bandlücke bezeichnet wird, von fünf bis zehn eV. Diese Lücke sorgt dann auch dafür, dass das Valenz- und das Leitungsband voneinander getrennt sind. Ist das Valenzband nun allerdings nur teilweise gefüllt, können sich die Elektronen durch die unbesetzten Zustände bewegen, wodurch der Körper zu einem Leiter wird. Weiterhin überlappen sich bei diesem das Valenz- und das Leitungsband, wobei sich hier die Elektronen allerdings im Leitungsband befinden und die Leitfähigkeit des vorliegenden Materials beeinflussen. Zuletzt existieren noch die sogenannten Halbleiter, bei der ebenfalls eine Bandlücke vorliegt, welche aber, anders als beim Isolator, nur eine Energie von rund einem eV beträgt. Dadurch ist es bei dieser Leiterart bereits mit wenig Energie möglich, die Elektronen dazu zu bringen in das Leitungsband zu springen.
2.1. Bestimmung der Schallgeschwindigkeit aus den Resonanzfrequenzen
Im ersten Versuchsteil soll die Schallgeschwindigkeit bestimmt werden. Dazu wurden in den beiden Ende des leeren Metallrohrs ein Lautsprecher und ein Mikrofon angebracht. Die Länge des Metallrohrs wurde zu messen. Mit dem Frequenzgenerator wurde dann eine Frequenz eingestellt die über den Lautsprecher ausgegeben wurde, welche schrittweise erhöht wurde und mit dem Oszilloskop wurde beobachtet, bei welchen Frequenzen Resonanzen, also lokale Maxima auftraten. Da es mit zunehmender Frequenz schwieriger wurde zu beurteilen, wo genau die Resonanzfrequenz liegt, wird für die Frequenz ein Fehler von verwendet und nur Resonanzfrequenzen bis ca. 10000 Hz aufgenommen. In der folgenden Abbildung sind die Resonanzfrequenzen über die Nummer der Resonanz aufgetragen (einzelne Werte sind im Messprotokoll zu finden).
Abbildung 1: Resonanzfrequenz im leeren Rohr
Mit der Nummer der Resonanz n und der Formel wird nun für jede Resonanz die Wellenzahl k berechnet. Für die erste Resonanz folgt eine Beispielrechnung.
Damit ergibt sich für die erste Resonanz eine Wellenzahl von . Die Werte für die übrigen Resonanzen sind in der folgenden Tabelle zu finden.
|
Resonanzfrequenz in Hz |
Wellenzahl in |
|
|
1 |
287 |
|
|
2 |
573 |
|
|
3 |
860 |
|
|
4 |
1147 |
|
|
5 |
1434 |
|
|
6 |
1721 |
|
|
7 |
2008 |
|
|
8 |
2295 |
|
|
9 |
2581 |
|
|
10 |
2869 |
|
|
11 |
3155 |
|
|
12 |
3444 |
|
|
13 |
3732 |
|
|
14 |
4019 |
|
|
15 |
4308 |
|
|
16 |
4592 |
|
|
17 |
4884 |
|
|
18 |
5167 |
|
|
19 |
5455 |
|
|
20 |
5745 |
|
|
21 |
6033 |
|
|
22 |
6325 |
|
|
23 |
6611 |
|
|
24 |
6902 |
|
|
25 |
7189 |
|
|
26 |
7484 |
|
|
27 |
7758 |
|
|
28 |
8053 |
|
|
29 |
8338 |
|
|
30 |
8633 |
|
|
31 |
8909 |
|
|
32 |
9203 |
|
|
33 |
9488 |
|
|
34 |
9782 |
|
|
35 |
10054 |
|
|
36 |
10361 |
|
Tabelle 1: Berechnete Wellenzahl
Als nächstes wird nun die Resonanzfrequenz f über die Wellenzahl aufgetragen.
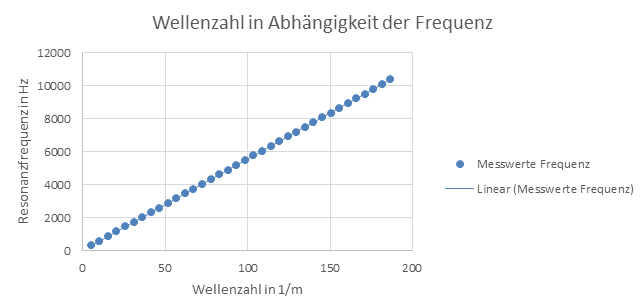
Abbildung 2: Wellenzahl in Abhängigkeit der Frequenz
Die Resonanzfrequenz in Abhängigkeit der Wellenzahl kann mit der Steigung m der Ausgleichsgeraden beschrieben werden als , wobei für die Steigung gilt, mit c als Schallgeschwindigkeit. Für die Steigung ergibt sich , woraus nun die Schallgeschwindigkeit berechnet werden kann.
Damit ergibt sich eine Schallgeschwindigkeit von
Im zweiten Versuchsteil wurden nun 12 Blenden in das Rohr geschoben und wieder die Resonanzfrequenzen gemessen. In der folgenden Abbildung sind die Resonanzfrequenzen über die Nummer der Resonanzen mit den Hülsen im Rohr aufgetragen.
Abbildung 3: Resonanzfrequenz mit Hülsen
Wie in der Abbildung zu sehen ist gibt es Frequenzbereiche (zwischen der zehnten und elften, sowie der 17. Und 18. Resonanz) in denen keine Resonanzfrequenzen auftreten. Die Größe dieser akustischen Bandlücken wird nun berechnet, indem die Differenz von der Frequenz vor der Bandlücke und der Frequenz nach der Bandlücke gebildet wird.
Damit ergeben sich die zwei Bandlücken von und .
2.3. Bestimmung der Wellenlänge
Formel (1.2.10) kann umgestellt werden zu , womit nun für die Resonanzen Nr. 12 und 24 die Wellenlängen berechnet werden.
Damit ergeben sich die zwei Wellenlängen von und . Vergleicht man diese Wellenlängen mit den Hülsenlängen, welche zu gemessen wurden, so ist zu erkennen, dass die Wellenlänge der 24. Resonanz der Hülsenlänge und die Wellenlänge der zwölften Resonanz der doppelten Hülsenlänge entspricht.
2.4. Effektive Schallunterdrückung
Im letzten Versuchsteil wurden in das leere Rohr nacheinander die Hülsen einzeln eingeschoben und bei jeder Hülse mit dem Ohr gelauscht, was in dem Rohr zu hören ist. Dabei wurden folgende Beobachtungen gemacht. Bei null Hülsen ist der Ton deutlich zu hören. Durch eine Hülse wird der Ton merklich abgeschwächt ist aber noch gut zu hören. Bei zwei Hülsen ist der Ton recht leise kann aber noch vom Ton neben dem Rohr unterschieden werden. Durch drei Hülsen nimmt man den Ton nur noch als leichtes Brummer war. Bei vier Hülsen hört man nur noch ein dumpfes Geräusch war, welches kaum noch von der Rohrschwingung unterscheidbar ist. Bei fünf Hülsen ist der Ton nicht mehr hörbar.
Die in diesem Versuch bestimmte Schallgeschwindigkeit von stimmt mit dem Literaturwert [3] von bei 20°C und 101,3 kPa nicht ganz überein. Da in einem anderen Versuch am selben Tag eine Temperatur im Versuchsraum von 27°C gemessen wurde und die Schallgeschwindigkeit mit der Temperatur zunimmt ist keine große Abweichung zu erwarten. Bei den Frequenzen der zwölften und 24. Resonanz fällt auf, dass diese Frequenz in der ersten bzw. zweiten Bandlücke liegt. Als Fehlerquelle in diesem Versuch kann betrachtet werden, dass bei großen Frequenzen auf dem Oszilloskop ein starkes Rauschen auftrat, was das Auslesen der Resonanzfrequenz schwer machte.
In diesem Versuch wurde die Schallgeschwindigkeit bestimmt zu
die zwei akustischen Bandlücken zu
und
sowie die Wellenlänger der zwölften und 24. Resonanz zu
- Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
- Georg-August-Universität Göttingen. (16. Juli 2015). Abgerufen am 16. Juli 2015 von Georg-August-Universität Göttingen: https://lp.uni-goettingen.de/get/text/6779
- Kuchling, H. (2014). Taschenbuch der Physik (21. Ausg.). München: Carl Hanser Verlag.
- Martin, A. P. (27. Mai 2015). LEIFIphysik. Abgerufen am 27. Mai 2015 von LEIFIphysik: http://www.leifiphysik.de/themenbereiche/mechanische-wellen/versuche
- Meschede, D. (2010). Gerthsen Physik (24. überarbeitete Ausg.). Springer-Verlag.
- Sengpielaudio. (kein Datum). Abgerufen am 19. September 2014 von Sengpielaudio: http://www.sengpielaudio.com/Rechner-schallgeschw.htm
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Ausg.). Springer-Verlag.
- Tipler, P. A., & Mosca, G. (16. Juli 2015). Springer. Abgerufen am 16. Juli 2015 von Springer: http://link.springer.com/chapter/10.1007/978-3-642-54166-7_37/fulltext.html
- Log in to post comments





Neueste Kommentare