Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls C-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Raster-Kraft-Makroskop
Inhaltsverzeichnis
Abbildung 1: Schwingfall
Abbildung 2: Kriechfall
Abbildung 3: Aperiodischer Grenzfall
Abbildung 4: Verschiebung der Resonanzfrequenz
Abbildung 5: Resonanzkurve
Abbildung 6: Phasenverschiebung
Abbildung 7: Grafische Darstellung der Phasendifferenz über die Oberfläche
Abbildung 8: Grafische Darstellung der Amplitude über die Oberfläche
Abbildung 9: Grafische Darstellung der Phasenverschiebung über die Oberfläche mit
Abbildung 10: Grafische Darstellung der Amplitude über die Oberfläche mit
Abbildung 11: Grafische Darstellung der Amplitude über die Oberfläche mit
Abbildung 12: Grafische Darstellung der Phasenverschiebung über die Oberfläche mit
Tabelle 1: Berechente Phasenverschiebung 1
Tabelle 2: Berechnete Phasenverschiebung 2
Tabelle 3: Gegebene Messwerte
In diesem Versuch ist das Ziel die nähere Betrachtung eines makroskopischen Analogons zu einem Raster-Kraft-Mikroskop.
Durch die Auslenkung eines Systems, welches sich im Gleichgewicht befindet, entsteht eine gedämpfte harmonische Schwingung. Die Schwingungsdifferentialgleichung für eine gedämpfte harmonische Drehschwingung lautet:
(1.2.1)
Wobei der Momentanbeschleunigung, der Momentangeschwindigkeit, y der Auslenkung, der Eigenfrequenz der gedämpften Schwingung und dem Abklingkoeffizienten entspricht. setzt sich dabei zusammen aus D, dem Dämpfungsmaß, und . Die während der Bewegung auftretende Reibung wirkt der Schwingung entgegen und bremst sie so immer weiter ab, bis sie schließlich vollständig zum Erliegen kommt. Die Schwingungsenergie wird dabei an die Umgebung übertragen. Die Zeit, welche bis zum Erliegen der Schwingung benötigt wird, ist maßgeblich von der Art der gedämpften Schwingungen abhängig. Es wird dabei zwischen den drei folgenden Schwingungsarten unterschieden. Bei dem ersten Fall, dem Schwingfall, entsteht, aufgrund einer geringer Dämpfung (), eine lange Schwingdauer und die Wiederherstellung des ursprünglichen Systemgleichgewichts stellt sich erst nach einem längeren Zeitraum wieder ein. Dem entgegen steht der zweite Fall, der Kriechfall, bei dem eine starke Dämpfung existiert (), weshalb das ausgelenkte System hier nur vergleichsweiße kurz schwingt, bis sich die Gleichgewichtslage wieder einstellt. Der dritte und auch letzte Fall, der aperiodische Grenzfall, stellt die schnellste Variante des Kriechfalls dar. Bei diesem erfolgt, aufgrund der Dämpfungsart (), fast überhaupt keine Schwingung wenn das System ausgelenkt wird und es kommt zu eine sehr schnelle Wiederherstellung des anfänglichen Gleichgewichts. Den grafischen Verlauf der jeweiligen Schwingfälle, kann den jeweiligen Abbildungen eins bis drei entnommen werden. Möchte man nun eine dauerhafte Schwingung erzeugen, so muss permanent Energie zugeführt werden, beispielsweise durch einen Motor. Bei einem gedämpften Oszillator folgt dann dafür die Gleichung:
(1.2.2)
dabei steht m für die Masse des Oszillators, d für die Dämpfungskonstante, a für eine beliebige Konstante und F für die anregende Kraft. Wenn nun die anregende Frequenz der Pendelfrequenz entspricht, dann entsteht der Resonanzfall. Bei diesem Fall wird die Pendelfrequenz durch die anregende Frequenz verstärkt und die Amplitude wird Maximal. Weiterhin erfolgt eine Phasenverschiebung von 90° zwischen der Schwingung und der anregenden Frequenz. Außerdem ist die Resonanzfrequenz bestimmbar mittels der Formel:
(1.2.3)
bei der k für die Federkonstante und für die effektive Masse steht. Da in diesem Versuch nur ein einseitig eingespannter Balken betrachtet wird, lässt sich die Federkonstante mit der folgenden Gleichung lösen:
(1.2.4)
wobei l für die Länge, b für die Breite, d für die Dicke und E für den Elastizitätsmodul des Balkens steht.
Durch permanente Magnete oder bewegte elektrische Ladungen werden Magnetfelder erzeugt, deren Feldlinien stets abgeschlossen sind, da es keine magnetischen Monopole gibt. Es lässt sich dabei zwischen der magnetischen Flussdichte und der magnetischen Feldstärke unterscheiden. Berechnet werden können sie mittels der Gleichung:
(1.3.1)
wobei die Permeabilität, auch magnetische Leitfähigkeit genannt, definiert ist als:
(1.3.2)
dabei ist die magnetische Feldkonstante die vom Material abhängige Permeabilitätszahl. Um das magnetische Feld selbst zu beschreiben verwendet man den magnetische Fluss , welcher durch die magnetische Flussdichte mittels eines Flächenintegrals wie folgt berechnet werden kann:
(1.3.3)
Dieses erzeugte Magnetfeld wird nun dazu genutzt den Metallbalken zu einer Schwingung anzuregen. Durch diese Schwingung wird nun der magnetische Fluss beeinflusst, wodurch eine, proportional zur Schwingungsamplitude, Spannung induziert wird, welche mit Hilfe eines Oszilloskops gemessen werden kann. Diese Induktionsspannung , welche auftritt wenn in der Fläche, die von einem Leiter umgeben ist, eine zeitliche Änderung des magnetischen Flusses stattfindet, kann auf Basis von Formel (1.3.3) berechnet werden mit:
(1.3.4)
Zusätzlich wird der Balken noch durch die Wechselwirkung zwischen der Probe und dem Magneten beeinflusst. Diese Wechselwirkung lässt sich in die attraktive und repulsive Wechselwirkung aufteilen und führt zu einer Verschiebung der Resonanzfrequenz, siehe auch Abbildung 4. Dabei verschiebt die attraktive Wechselwirkung (rot) sie zu einer niedrigeren Frequenz und die repulsive Wechselwirkung (blau) zu einer höheren Frequenz. Durch diese Frequenzänderung kommt auch eine Änderung der Schwingungsamplitude zustande, allerdings sagt diese nichts über die Richtung, in die sich die Resonanzfrequenz bewegt, aus. Der Grund dafür ist der, dass die Amplitude bei beiden Wechselwirkungen kleiner wird und man deshalb die Phasenverschiebung betrachten muss. Dadurch ist es dann möglich die Verschiebungsrichtung der Resonanzfrequenz zu bestimmen, da bei einer positiven Phasenverschiebung sich die Frequenz nach links und bei einer Negativen sich die Frequenz nach rechts bewegt. So kann dann auch bestimmen, welche Wechselwirkung genau vorliegt. Berechnet werden kann die Phasenverschiebung mit der Gleichung:
(1.4.1)
Weiterhin kann man, wenn die Resonanzfrequenz kleiner als die Anregungsfrequenz ist, die Art der Wechselwirkung sowohl über die Phasenverschiebung als auch die Amplitude feststellen. Dazu vergleicht man die neue Amplitude, mit der alten Amplitude, welche bei derselben Frequenz ermittelt wird. Ist die neue Amplitude kleiner als die Alte, dann liegt eine attraktive Wechselwirkung vor und wenn sie größer ist, dann eine Repulsive. Dies funktioniert mit der Phasenverschiebung ähnlich, hier steht aber eine größere Verschiebung für die attraktive und eine kleiner Verschiebung für eine repulsive Wechselwirkung.
2.1. Schwingungsverhalten des Balkens
Im ersten Versuchsteil wurde die Spule des Balkens über den Verstärker mit dem Frequenzgenerator verbunden und so der Balken zu Schwingung angeregt. Nach dem Anschließen des Oszilloskops konnte beobachtet werden, dass die Schwingung des Balkens nicht exakt einer Sinuskurve folgte, sondern im Graph noch ein zusätzlicher Knick zu sehen war, da der Balken schon leicht verbogen war. Durch Variation der angelegten Spannung wurde die maximale Amplitude, also die Resonanzfrequenz bestimmt zu . Wurde eine Probe mit repulsiver Wechselwirkung zur Balkenspitze in die Nähe gebracht, konnte beobachtet werden, dass sich die Resonanzfrequenz nach rechts, also zu höheren Frequenzen verschiebt, während Proben mit attraktiver Wechselwirkung die Resonanzfrequenz nach links, also zu niedrigeren Frequenzen verschiebt.
2.2. Resonanz- und Phasenverschiebungskurve
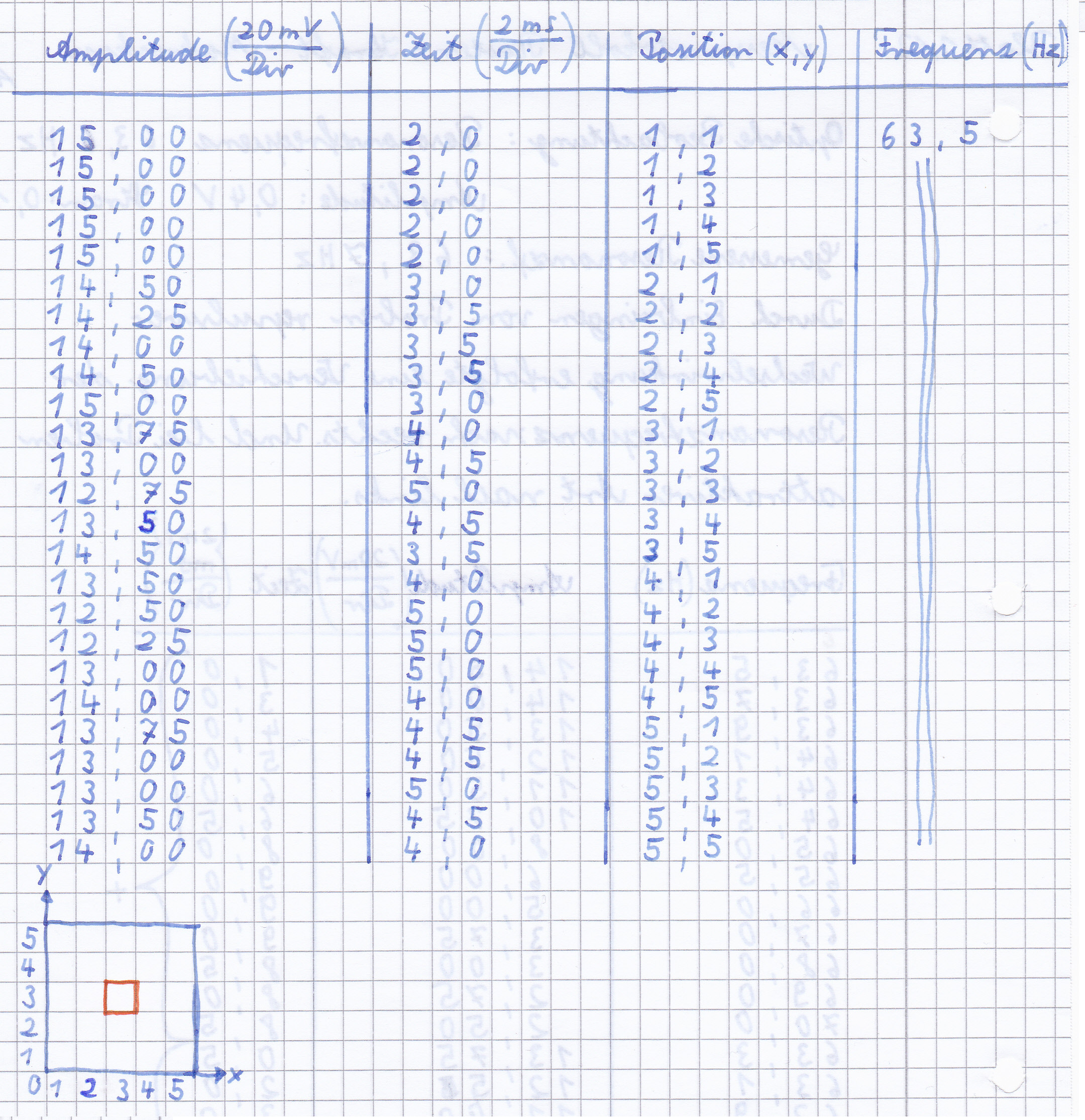
Im zweiten Versuchsteil wurden nun die Amplitude der in der zweiten Spule induzierten Spannung und die Verschiebung auf der Zeit-Achse zwischen angelegter und induzierter Spannung gemessen, während die Frequenz variiert wurde, wobei in der Nähe der Resonanzfrequenz die Frequenz in kleineren Schritten verändert wurde. Zu beachten ist, dass bei allen auf dem Messprotokoll in Divisions gemessenen Werten die kleinen Teilstiche auf dem Oszilloskop gezählt wurden und demnach noch durch 5 geteilt werden müssen. Trägt man nun die induzierte Spannung über die Frequenz auf so ergibt sich folgende Resonanzkurve.
Die Resonanzfrequenz liegt bei , je weiter man sich von dieser Frequenz entfernt, desto weiter nimmt die Amplitude ab. Im Folgenden soll die Phasenverschiebung bestimmt werden, wofür die zeitliche Verschiebung t zwischen angelegter und induzierter Spannung gemessen wurde. In diesem Versuch wurde bei der Resonanzfrequenz auch eine zeitliche Verschiebung gemessen, obwohl diese Null seien sollte, vermutlich hervorgerufen durch die Verbiegung des Balkens. Die Phasenverschiebung lässt sich berechnen mit der Formel (1.4.1):
Eine Beispielrechnung erfolgt für die erste Messung:
|
|
|
|
|
63,5 |
0,0004 |
|
|
63,7 |
0,0012 |
|
|
63,9 |
0,0016 |
|
|
64,1 |
0,002 |
|
|
64,3 |
0,0024 |
|
|
64,5 |
0,0026 |
|
|
65 |
0,0032 |
|
|
65,5 |
0,0036 |
|
|
66 |
0,0036 |
|
|
67 |
0,0036 |
|
|
68 |
0,0034 |
|
|
69 |
0,0032 |
|
|
70 |
0,0034 |
|
|
63,3 |
-0,0002 |
|
|
63,1 |
-0,0008 |
|
|
62,9 |
-0,0012 |
|
|
62,7 |
-0,0018 |
|
|
62,5 |
-0,0022 |
|
|
62 |
-0,0026 |
|
|
61,5 |
-0,0032 |
|
|
61 |
-0,0034 |
|
|
60 |
-0,0038 |
|
|
59 |
-0,004 |
|
|
58 |
-0,0042 |
|
|
57 |
-0,0044 |
In der folgenden Abbildung wird nun die Phasenverschiebung über die anregende Frequenz aufgetragen.
Wie in der Abbildung zu sehen ist, ändert sich die Phasenverschiebung im Bereich der Resonanzfrequenz stark mit der Frequenz, wohingegen sich die Phasenverschiebung entfernt von der Resonanzfrequenz kaum noch ändert. In einem Phasenverschiebungsdiagramm findet man gewöhnlich die Resonanzfrequenz bei einer Phasenverschiebung von 90° bzw. , in diesem Diagramm ist diese jedoch bei einer Phasenverschiebung von ungefähr 0 zu finden. Dies folgt daraus, dass die 90° Phasenverschiebung kompensiert wird, durch die Phasenverschiebung von 90° welche zwischen der angelegten und induzierten Spannung vorliegt.
In diesem Versuchsteil wurde der Balken mit der Resonanzfrequenz angeregt und über jedem Feld der 5x5 Felder großen Oberfläche die Amplitude und zeitliche Verschiebung gemessen. Eine Zeichnung der Oberfläche ist dem Messprotokoll zu entnehmen, im mittleren Feld der Fläche befindet sich ein Magnet. Die Berechnung der Phasenverschiebung erfolgt analog zu der Berechnung in Abschnitt 2.2.
|
x-Koordinate |
y-Koordinate |
|
|
in rad |
|
1 |
1 |
60 |
0,0008 |
|
|
1 |
2 |
60 |
0,0008 |
|
|
1 |
3 |
60 |
0,0008 |
|
|
1 |
4 |
60 |
0,0008 |
|
|
1 |
5 |
60 |
0,0008 |
|
|
2 |
1 |
58 |
0,0012 |
|
|
2 |
2 |
57 |
0,0014 |
|
|
2 |
3 |
56 |
0,0014 |
|
|
2 |
4 |
58 |
0,0014 |
|
|
2 |
5 |
60 |
0,0012 |
|
|
3 |
1 |
55 |
0,0016 |
|
|
3 |
2 |
52 |
0,0018 |
|
|
3 |
3 |
51 |
0,0020 |
|
|
3 |
4 |
54 |
0,0018 |
|
|
3 |
5 |
58 |
0,0014 |
|
|
4 |
1 |
54 |
0,0016 |
|
|
4 |
2 |
50 |
0,0020 |
|
|
4 |
3 |
49 |
0,0020 |
|
|
4 |
4 |
52 |
0,0020 |
|
|
4 |
5 |
56 |
0,0016 |
|
|
5 |
1 |
55 |
0,0018 |
|
|
5 |
2 |
52 |
0,0018 |
|
|
5 |
3 |
52 |
0,0020 |
|
|
5 |
4 |
54 |
0,0018 |
|
|
5 |
5 |
56 |
0,0016 |
In Abbildung 7 wird die Amplitude über der Oberfläche mit Gnu Plot grafisch dargestellt.
In Abbildung 8 wird für die gleiche Messung die Phasendifferenz über der Oberfläche aufgetragen.
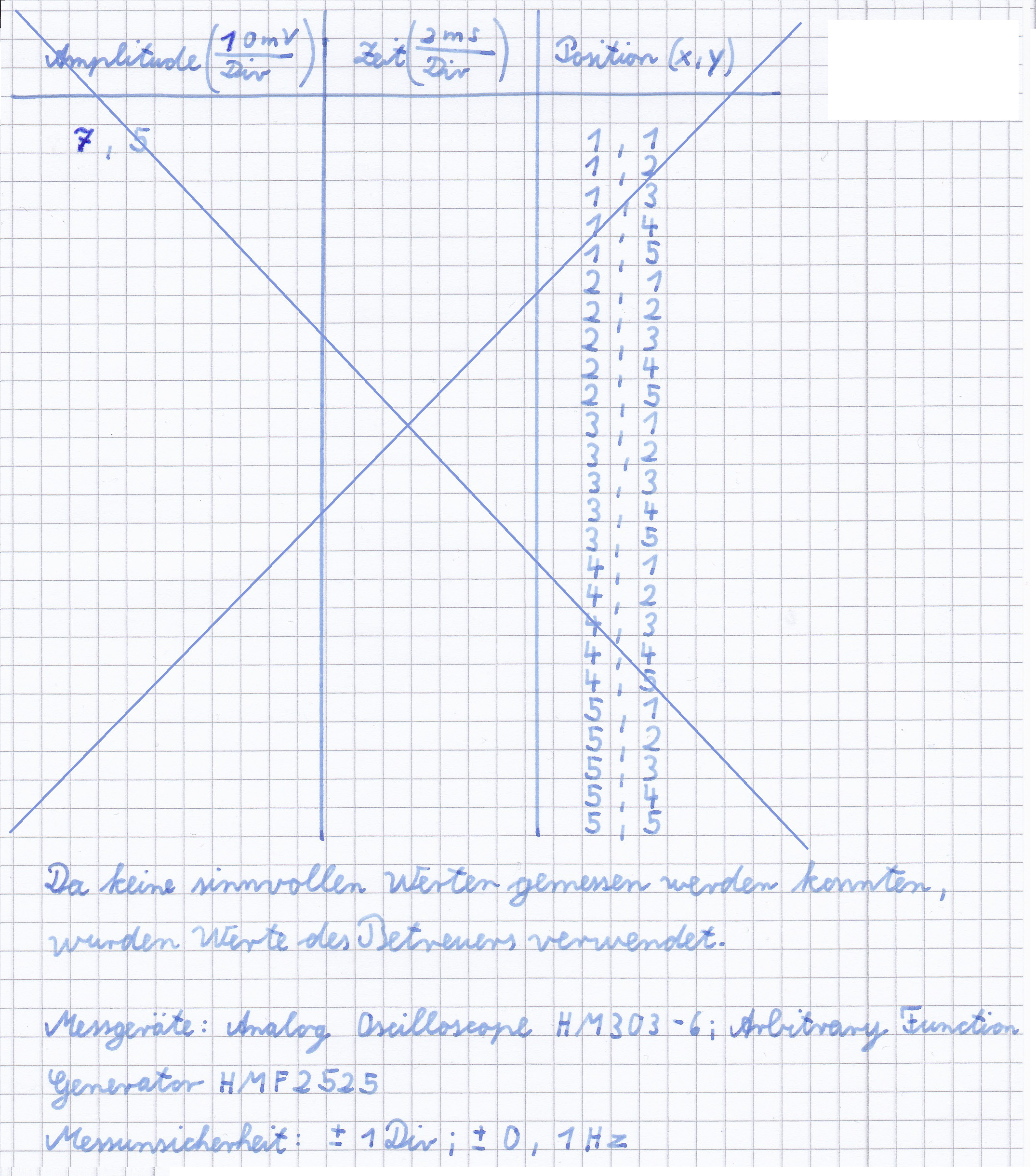
Es ist zu erkennen, dass an der Position des Magneten (3|3) im Gegensatz zum Rest der Fläche die Amplitude kleiner und die Phasenverschiebung größer ist. Die Amplitude ist in 2 angrenzenden Felder noch geringer, dies könnte auf unbekannte äußere Einflüsse hinweisen, berücksichtigt man jedoch die in der 3D Darstellung nicht sichtbaren Fehler, so sind diese Amplituden nicht zwangsweise kleiner als direkt über dem Magneten. Für die Phasenverschiebung wurden nur positive Werte gemessen, also sind nur attraktive Wechselwirkungen aufgetreten. Je weiter man sich von dem Magneten entfernt, desto weniger wird die Amplitude beeinflusst, bei den Feldern mit der Koordinate x=1 ist die Amplitude nahezu unverändert. Nach der Messung mit der Resonanzfrequenz sollte die gleiche Fläche noch einmal mit einer niedrigeren Frequenz gerastert werde, allerdings war das Signal auf dem Oszilloskop so undeutlich, dass überhaupt keine Veränderung der Amplitude gemessen werden konnte. Aus diesem Grund werden alte Messwerte des Betreuers verwendet. In der folgenden Tabelle sind diese Wert zu finden.
|
x-Koordinate |
y-Koordinate |
|
|
||
|
|
|
|
|
||
|
1 |
1 |
180 |
-0,08 |
120 |
0,48 |
|
1 |
2 |
185 |
-0,04 |
115 |
0,52 |
|
1 |
3 |
185 |
0,04 |
110 |
0,52 |
|
1 |
4 |
180 |
0,12 |
100 |
0,56 |
|
1 |
5 |
180 |
0,12 |
100 |
0,56 |
|
2 |
1 |
180 |
-0,08 |
105 |
0,52 |
|
2 |
2 |
185 |
-0,04 |
110 |
0,52 |
|
2 |
3 |
185 |
0,08 |
100 |
0,56 |
|
2 |
4 |
180 |
0,19 |
95 |
0,56 |
|
2 |
5 |
180 |
0,15 |
100 |
0,56 |
|
3 |
1 |
180 |
-0,08 |
110 |
0,52 |
|
3 |
2 |
180 |
-0,08 |
105 |
0,52 |
|
3 |
3 |
180 |
-0,08 |
105 |
0,52 |
|
3 |
4 |
180 |
-0,08 |
100 |
0,52 |
|
3 |
5 |
180 |
-0,08 |
100 |
0,52 |
|
4 |
1 |
180 |
-0,08 |
105 |
0,52 |
|
4 |
2 |
180 |
-0,15 |
105 |
0,52 |
|
4 |
3 |
170 |
-0,27 |
110 |
0,52 |
|
4 |
4 |
170 |
-0,27 |
105 |
0,52 |
|
4 |
5 |
170 |
-0,27 |
100 |
0,52 |
|
5 |
1 |
180 |
-0,12 |
95 |
0,52 |
|
5 |
2 |
175 |
-0,15 |
100 |
0,52 |
|
5 |
3 |
170 |
-0,35 |
105 |
0,52 |
|
5 |
4 |
165 |
-0,39 |
100 |
0,52 |
|
5 |
5 |
170 |
-0,35 |
100 |
0,52 |
Die folgenden zwei Abbildungen zeigen die 3D Darstellung der Amplitude über der Oberfläche und der Phasenverschiebung über der Oberfläche mit der Resonanzfrequenz .
In den beiden Abbildungen kann man sehen, dass hautsächlich der mittlere Teil der Fläche, bei der Amplitude ohne Magneten, bzw. einer Phasenverschiebung von ungefähr 0 liegt, also kaum Wechselwirkungen stattfinden. Auf der Feld (5|5) und auf angrenzenden Feldern kann man eine negative Phasenverschiebung erkenne, also repulsive Wechselwirkung, während auf dem Feld (1|5) und den angrenzenden Feldern eine positive Phasenverschiebung, also attraktive Wechselwirkung zu erkennen ist. Wahrscheinlich werden die beiden verschiedenen Wechselwirkungen durch die beiden Pole des Magneten hervorgerufen. Die nächsten zwei Abbildungen zeigen die 3D Darstellung der Amplitude über der Oberfläche und der Phasenverschiebung über der Oberfläche mit der Frequenz .
In der Abbildung der Amplitude lässt sich wie bei der Resonanzfrequenz erkennen, dass die Amplitude bei (1|1) größer ist und zu (5|5) kleiner wird, allerdings ist bei ungefähr (4|3) noch eine Erhöhung und bei ungefähr (2|4) eine Vertiefung zu erkennen. Aus dieser Abbildung geht nicht ganz klar hervor, wie der Magnet orientiert sein könnte, es könnten noch andere äußere Einflüsse aufgetreten sein. Die Abbildung der Phasendifferenz sieht der Abbildung mit der Resonanzfrequenz ähnlich, ein Teil der Fläche liegt wieder auf einer Ebene und größere Phasendifferenzen treten wieder in (1|5) und den angrenzenden Feldern auf, allerdings sind bei dieser Messung alle Phasendifferenzen positiv und es findet somit nur attraktive Wechselwirkung statt.
Die durch Variation der Frequenz bestimmte Resonanzfrequenz wurde per Augenmaß zu 63,6 bestimmt. Auch die Resonanz- und Phasenverschiebungskurve lassen nicht darauf schließen, dass die Resonanzfrequenz stark von dem bestimmten Wert abweicht. Trotzdem gab es bei diesem Versuch einige Fehlerquellen. Wie schon beschrieben war der Balken schon zu Beginn des Versuchs verbogen, sodass am Oszilloskop ein Knick in der ansonsten Sinus förmigen Kurve vorhanden war, was zu einem veränderten Schwingungsverhalten geführt haben könnte. Außerdem wurde beobachtet, dass sich die Kurve leicht veränderte, als man den Balken anhob, was durch Metallstreben hervorgerufen worden sein könnte, welche an der Unterseite des Tisches verliefen. Eine leichte Veränderung konnte auch beobachtet werden, als man den Balken in die Nähe der Messgeräte brachte. Außerdem befanden sich in der Platte, auf der ein Teil der Oberfläche gerastert wurde, weitere Magnete, welche für zusätzliche Wechselwirkungen verantwortlich sein könnten.
In diesem Versuch wurde die Resonanzfrequenz des Balkens bestimmt zu:
Und beim Rastern der Oberfläche verschiedene Wechselwirkungen durch Magneten festgestellt.
- Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
- Erdmann, M. (2011). Physik Denken - Exprimentalphysik 3 - Schwingungen, Wellen, Körperdrehungen (1. Ausg.). Springer-Verlag.
- Georg-August-Universität Göttingen. (5. Juli 2015). Abgerufen am 5. Juli 2015 von Georg-August-Universität Göttingen: https://lp.uni-goettingen.de/get/text/4622
- Goertz, S. (kein Datum). Universität Bonn. Abgerufen am 2. September 2014 von Universität Bonn: http://pi.physik.uni-bonn.de/~goertz/Blockseminar/Versuch6.pdf
- Kraus, D., & Pieper, W. (kein Datum). Hochschule Bremen. Abgerufen am 2. September 2014 von Hochschule Bremen: http://homepages.hs-bremen.de/~krausd/iwss/V5a.pdf
- Kuchling, H. (2014). Taschenbuch der Physik (21. Ausg.). München: Carl Hanser Verlag.
- NDT Resource Center. (5. Juli 2015). Abgerufen am 5. Juli 2015 von NDT Resource Center: https://www.nde-ed.org/EducationResources/CommunityCollege/MagParticle/…
- Tipler, P. A. (2000). Physik (3. korrigierte Ausg.). Spektrum Akademischer Verlag.
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Ausg.). Springer-Verlag.
- Wedler, G., & Freund, H.-J. (2012). Lehrbuch der physikalischen Chemie (6. vollständig überarbeitete und aktualisierte Ausg.). WILEY-VCH Verlag GmbH & Co. KGaA.
- Wikipedia. Abgerufen am 10. Juni 2015 von Wikipedia: https://de.wikipedia.org/wiki/Magnetische_Suszeptibilit%C3%A4t
- Wikipedia. Abgerufen am 10. Juni 2015 von Wikipedia: https://de.wikipedia.org/wiki/Magnetismus